
题目列表(包括答案和解析)
我们给出如下定义:若四边形中一对顶点到另一对顶点所连的对角线的距离相等,则把这对顶点叫做这个四边形的一对等高点.例如:如图,在□ABCD中,可证点A、C到BD的距离相等,所以点A、C是□ABCD的一对等高点,同理可知点B、D也是□ABCD的一对等高点.
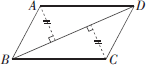
(1)如图,已知□ABCD,请你在图中画出一个只有一对等高点的四边形ABCE;(要求画出必要的辅助线)
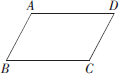
(2)已知点P是四边形ABCD的对角线BD上任意一点(不与点B、D重合),请分别探究图、下图中S1、S2、S3、S4四者之间的等量关系(S1、S2、S3、S4分别表示△ABP、△CBP、△CDP、△ADP的面积)
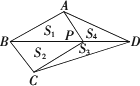
①如上图,当四边形ABCD只有一对等高点A、C时,你得到的一个结论是________;
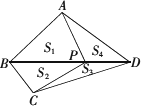
②如图,当四边形ABCD没有等高点时,你得到的一个结论是________.
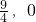 ),与
),与 双曲线
双曲线 (x>0)交于点B.
(x>0)交于点B.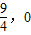 ),与双曲线
),与双曲线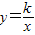 (x>0)交于点B.
(x>0)交于点B.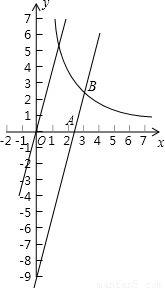
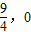 ),与双曲线
),与双曲线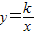 (x>0)交于点B.
(x>0)交于点B.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com