实验探究：

(1)动手操作：

①如图1，将一块直角三角板DEF放置在直角三角板ABC上，使三角板DEF的两条直角边DE、DF分别经过点B、C，且BC∥EF，已知∠A＝30°，则∠ABD＋∠ACD＝________°；

②如图2，若直角三角板ABC不动，改变等腰直角三角板DEF的位置，使三角板DEF的两条直角边DE、DF仍然分别经过点B、C，已知∠A＝30°，那么∠ABD＋∠ACD＝________°；

(2)猜想证明：

如图3，∠BDC与∠A、∠B、∠C之间存在着什么关系，并说明理由；

(3)灵活应用：

请你直接利用以上结论，解决以下列问题：

①如图4，BE平分∠ABD，CE平分∠ACD，若∠BAC＝40°，∠BDC＝120°，求∠BEC的度数；

②如图5，∠ABD、∠ACD的10等分线相交于点F₁、F₂、…、F₉，若∠BDC＝120°，∠BF₃C＝64°，求∠A的度数．

已知：△ABC的高AD所在直线与高BE所在直线相交于点F．

(1)如下图，若△ABC为锐角三角形，且∠ABC＝45°，过点F作FG∥BC，交直线AB于点G，求证：FG＋DC＝AD；

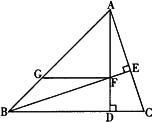
(2)如下图，若∠ABC＝135°，过点F作FG∥BC，交直线AB于点G，则FG、DC、AD之间满足的数量关系是；

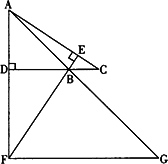
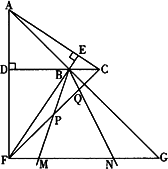
(3)在(2)的条件下，若AG＝5，DC＝3，将一个45°角的顶点与点B重合并绕点B旋转，这个角的两边分别交线段FG于M、N两点(如下图)，连接CF，线段CF分别与线段BM、线段BN相交于P、Q两点，若NG＝，求线段PQ的长．

如图，抛物线y＝ax²－2ax＋c(a≠0)交x轴于A、B两点，A点坐标为(3，0)，与y轴交于点C(0，4)，以OC、OA为边作矩形OADC交抛物线于点G．

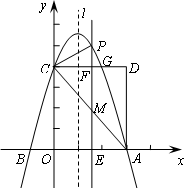
(1)求抛物线的解析式；

(2)抛物线的对称轴l在边OA(不包括O、A两点)上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长．

(3)在(2)的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由．