
题目列表(包括答案和解析)
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲 |
| AB |
|
|
|
|
|
|
| n(2n-1) |
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
|
| π |
| 4 |
| 2 |
|
 A.如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,DE交AB于点F.求证:△PDF∽△POC.
A.如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,DE交AB于点F.求证:△PDF∽△POC.
|
|
| π |
| 4 |
| 2 |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
.P是双曲线 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
A. 6 B.7 C.8 D.9
.P是双曲线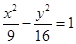 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
A. 6 B.7 C.8 D.9
一、选择题
BBACA DCBBB(分类分布求解)
二、填空题
11.{2,7} 12.840 13.1 14.2 15.--理科数学.files/image014.gif) (圆锥曲线定义)
(圆锥曲线定义)
16.解:(1)由--理科数学.files/image110.gif)
(2)由余弦定理知:--理科数学.files/image112.gif)
又--理科数学.files/image114.gif)
17.解:设事件A为“小张被甲单位录取”,B为“被乙单位录取”,C为“被丙单位录取”。
(1)小张没有被录取的概率为:--理科数学.files/image116.gif)
(2)小张被一个单位录取的概率为--理科数学.files/image118.gif)
被两个单位同时录取的概率为--理科数学.files/image120.gif)
被三个单位录取的概率为:--理科数学.files/image122.gif) 所以分布列为:
所以分布列为:
ξ
0
1
2
3
P
--理科数学.files/image124.gif)
--理科数学.files/image126.gif)
--理科数学.files/image128.gif)
--理科数学.files/image130.gif)
所以:--理科数学.files/image132.gif)
18.解:(1)--理科数学.files/image134.gif)
--理科数学.files/image136.gif)
|