
题目列表(包括答案和解析)
商场销售某种商品的经验表明,该商品每日的销售量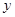 (单位:千克)与销售价格
(单位:千克)与销售价格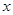 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式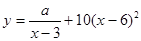 ,其中
,其中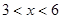 ,
,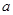 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求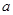 的值;
的值;
(2) 若商品的成品为3元/千克, 试确定销售价格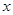 的值,使商场每日销售该商品所获得的利润最大
的值,使商场每日销售该商品所获得的利润最大
【解析】(1)利用销售价格为5元/千克时,每日可售出该商品11千克.把x=5,y=11代入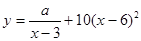 ,解关于a的方程即可求a..
,解关于a的方程即可求a..
(2)在(1)的基础上,列出利润关于x的函数关系式,
利润=销售量 (销售单价-成品单价),然后利用导数求其最值即可.
(销售单价-成品单价),然后利用导数求其最值即可.
已知函数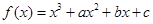 ,曲线
,曲线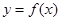 在点
在点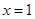 处的切线为
处的切线为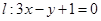 ,若
,若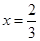 时,
时,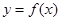 有极值.
有极值.
(1)求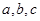 的值;
的值;
(2)求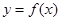 在
在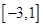 上的最大值和最小值.
上的最大值和最小值.
【解析】(1)根据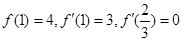 可建立关于a,b,c的三个方程,解方程组即可.
可建立关于a,b,c的三个方程,解方程组即可.
(2)在(1)的基础上,利用导数列表求极值,最值即可.
(本小题满分12分)
已知函数 ;
;
(1)求 ; (2)求
; (2)求 的最大值与最小值.
的最大值与最小值.
【解析】第一问利用导数的运算法则,幂函数的导数公式,可得。
第二问中,利用第一问的导数,令导数为零,得到
然后结合导数,函数的关系判定函数的单调性,求解最值即可。
已知函数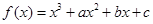 在
在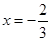 与
与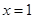 时都取得极值.
时都取得极值.
(1)求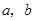 的值及函数
的值及函数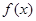 的单调区间;www.7caiedu.cn
的单调区间;www.7caiedu.cn
(2)若对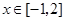 ,不等式
,不等式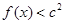 恒成立,求
恒成立,求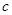 的取值范围.
的取值范围.
【解析】根据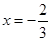 与
与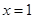 是
是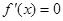 的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
的两个根,可求出a,b的值,然后利用导数确定其单调区间即可.
(2)此题本质是利用导数其函数f(x)在区间[-1,2]上的最大值,然后利用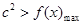 ,即可解出c的取值范围.
,即可解出c的取值范围.
已知函数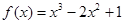 .
.
(1)求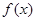 在区间
在区间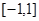 上的最大值;
上的最大值;
(2)若函数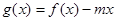 在区间
在区间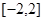 上存在递减区间,求实数m的取值范围.
上存在递减区间,求实数m的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用,求解函数的最值。第一问中,利用导数求解函数的最值,首先求解导数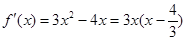 ,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在
,然后利用极值和端点值比较大小,得到结论。第二问中,我们利用函数在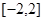 上存在递减区间,即
上存在递减区间,即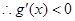 在
在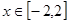 上有解,即
上有解,即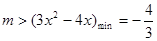 ,即可,可得到。
,即可,可得到。
解:(1)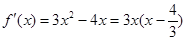 ,
,
令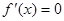 ,解得
,解得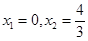 ……………3分
……………3分
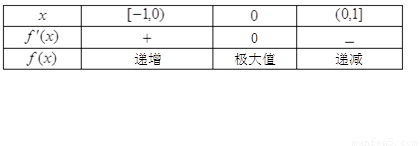
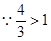 ,
,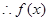 在
在 上为增函数,在
上为增函数,在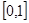 上为减函数,
上为减函数,
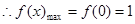 .
…………6分
.
…………6分
(2)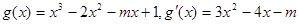
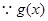 在
在 上存在递减区间,
上存在递减区间,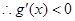 在
在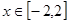 上有解,……9分
上有解,……9分
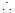
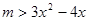 在
在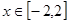 上有解,
上有解,
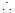
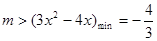 ,
,
所以,实数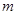 的取值范围为
的取值范围为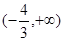
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com