如右图所示，电阻R=1Ω、半径r₁=0.2m的单匝圆形导线框P内有一个与P共面的圆形磁场区域Q，P、Q的圆心相同，Q的半径r₂=0.1m。t=0时刻，Q内存在着垂直于圆面向里的磁场，磁感应强度B随时间t变化的关系是B=2-t（T）。若规定逆时针方向为电流的正方向，则线框P中感应电流I随时间t变化的关系图象应该是下图中的（   ）

如右图所示，电阻R=1Ω、半径r₁=0.2m的单匝圆形导线框P内有一个与P共面的圆形磁场区域Q，P、Q的圆心相同，Q的半径r₂=0.1m。t=0时刻，Q内存在着垂直于圆面向里的磁场，磁感应强度B随时间t变化的关系是B=2-t（T）。若规定逆时针方向为电流的正方向，则线框P中感应电流I随时间t变化的关系图象应该是下图中的（   ）

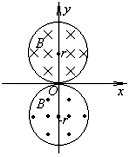两个圆形区域内存在着匀强磁场，这两个圆的半径都是r，圆心都在y轴上，两圆相切，切点恰是原点O．两圆内磁场的磁感强度大小相同，但方向相反，上面的沿-z方向，下面的沿+z方向，如图所示．在坐标原点O处有一个放射源，放射出质量为m、电量为-q的带电粒子(重力不计)，如果所有粒子都在xOy平面内，初速度大小都是v₀，并且向各个方向的发射是均匀的．不计各粒子在运动过程中的相互作用．

 (1)调整磁场磁感强度的大小，可以使得所有的粒子(除了沿-x方向运动的极少数粒子以外，下同)，经过磁场的偏转后速度方向都互相平行，求这时的磁感强度B的值．

(2)在满足上述条件的情况下，在x轴右方较远处与y轴平行的屏上接收到的粒子都位于与y轴平行的一条线段上，其中y=o到y=a间的区域内的粒子数是全部粒子数的1/6，求a的值．

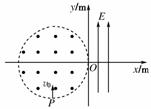
在如右图所示的平面直角坐标系中，存在一个半径R＝0.2m的圆形匀强磁场区域，磁感应强度B＝1.0T，方向垂直纸面向外，该磁场区域的右边缘与坐标原点O相切．y轴右侧存在电场强度大小为E＝1.0×10⁴N/C的匀强电场，方向沿y轴正方向，电场区域宽度l＝0.1m．现从坐标为(－0.2m，－0.2m)的P点发射出质量m＝2.0×10^－9kg、带电荷量q＝5.0×10^－5C的带正电粒子，沿y轴正方向射入匀强磁场，速度大小v₀＝5.0×10³m/s.重力不计．

(1)求该带电粒子射出电场时的位置坐标；

(2)为了使该带电粒子能从坐标为(0.1m，－0.05m)的点回到电场后，可在紧邻电场的右侧一正方形区域内加匀强磁场，试求所加匀强磁场的磁感应强度大小和正方形区域的最小面积．