练习册

  • 练习册
  • 试题
    可求得a= -1. 【查看更多】

     

    题目列表(包括答案和解析)

    设A={1，2，…，18}. 求最小的正整数k，使得可以把集合A分成k个两两不交的子集A1，A2，…，Ak，对于任一子集）中的任意3个数a，b，c（可以是相同的），都有

    查看答案和解析>>

    （1）已知抛物线y2=2px（p＞0），过焦点F的动直线l交抛物线于A，B两点，为坐标原点，求证：
    OA
    •
    OB
    为定值；
    （2）由（1）可知：过抛物线的焦点F的动直线l交抛物线于A，B两点，存在定点P，使得
    PA
    •
    PB
    为定值．请写出关于椭圆的类似结论，并给出证明．

    查看答案和解析>>

    设
    a
    =(
    		3
    sinx，cosx)    ，
    b
    =(cosx，cosx)    ，记f(x)=
    a
    •
    b
    ．
    （1）写出函数f（x）的最小正周期；
    （2）试用“五点法”画出函数f（x）在区间[-
    π
    12
    ，
    11π
    12
    ]    的简图，并指出该函数的图象可由y=sinx（x∈R）的图象经过怎样的平移和伸缩变换得到？
    （3）若x∈[-
    π
    6
    ，
    π
    3
    ]    时，函数g（x）=f（x）+m的最小值为2，试求出函数g（x）的最大值并指出x取何值时，函数g（x）取得最大值．

    查看答案和解析>>

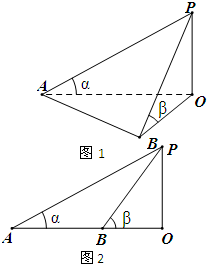    如图1，某学校田径场上有一旗杆OP，为了测量它的高度，在地面上选一基线AB，设其长度为d，在A点处测得P点的仰角为α，在B点处测得P点的仰角为β．
    （1）若AB=20，α=30°，β=45°，且∠AOB=30°，求旗杆的高度h；
    （2）经分析若干测得的数据后，发现将基线AB调整到线段AO上（如图2），α与β之差尽量大时，可以提高测量精确度，设调整后AB的距离为d，tanβ=
    4d
    ，旗杆的实际高度为25，试问d为何值时，β-α最大？

    查看答案和解析>>

    （1）以正方体的顶点为顶点，可以确定多少个四棱锥？
    （2）黑暗中从3双尺码不同的鞋子中任意摸出3只，求摸出3只中有配成一双（事件A）的概率．
    （3）利用二项式定理求1432013被12除所得的余数．

    查看答案和解析>>


    同步练习册答案