
5.若α,β是一组基底,向量γ=x·α+y·β(x,y∈R),则称(x,y)为向量γ在基底α,β下的坐标,现已知向量a在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a在另一组基底m=(-1,1),n=(1,2)下的坐标为 ( )
A.(2,0) B.(0,-2)
C.(-2,0) D.(0,2)
解析:由已知a=-2p+2q=(-2,2)+(4,2)=(2,4),
设a=λm+μn=λ(-1,1)+μ(1,2)=(-λ+μ,λ+2μ),
则由⇒,
∴a=0m+2n,∴a在基底m,n下的坐标为(0,2).
答案:D
4.在三角形ABC中,已知A(2,3),B(8,-4),点G(2,-1)在中线AD上,且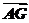 =2
=2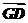 ,则点C的坐标是
( )
,则点C的坐标是
( )
A.(-4,2) B.(-4,-2)
C.(4,-2) D.(4,2)
解析:设C(x,y),则D(,),再由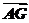 =2
=2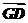 得(0,-4)=2(,),∴4+x=0,-2+y=-4,即C(-4,-2).
得(0,-4)=2(,),∴4+x=0,-2+y=-4,即C(-4,-2).
答案:B
3.在▱ABCD中, =a,
=a,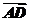 =b,
=b,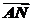 =3
=3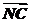 ,M为BC的中点,则
,M为BC的中点,则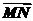 =________(用a、b表示).
=________(用a、b表示).
解析:由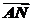 =3
=3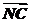 得4
得4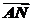 =3
=3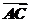 =3(a+b),
=3(a+b),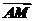 =a+b,所以
=a+b,所以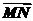 =(a+b)-(a+b)=-a+b.
=(a+b)-(a+b)=-a+b.
答案:-a+b
|
题组二 |
平面向量的坐标运算 |
2.(2010·温州模拟)已知直角坐标平面内的两个向量a=(1,3),b=(m,2m-3),使平平面内的任意一个向量c都可以唯一的表示成c=λa+μb,则m的取值范围是________.
解析:∵c可唯一表示成c=λa+μb,
∴a与b不共线,即2m-3≠3m,
∴m≠-3.
答案:{m∈R|m≠-3}
1.在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F.若
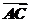 =a,
=a, =b,则
=b,则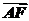 =
( )
=
( )
A.a+b B.a+b C.a+b D.a+b
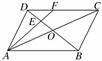 解析:如图所示,由△DEF∽△BEA知
解析:如图所示,由△DEF∽△BEA知
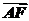 =
=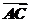 +
+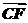 =a+
=a+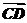
=a+(b-a)
=a+b.
答案:B
12.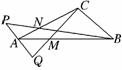 (文)如图,△ABC中,在AC上取一点N,使得AN=AC,
(文)如图,△ABC中,在AC上取一点N,使得AN=AC,
在AB上取一点M,使得AM=AB,在BN的延长线上取
点P,使得NP=BN,在CM的延长线上取点Q,使得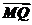 =λ
=λ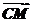 时,
时,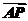 =
=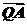 ,试确定λ的值.
,试确定λ的值.
解:∵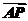 =
=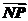 -
-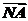 =(
=(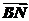 -
-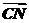 )
)
=(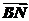 +
+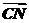 )=
)=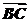 ,
,
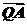 =
=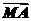 -
-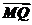 =
=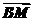 +λ
+λ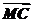 ,
,
又∵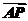 =
=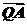 ,∴
,∴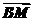 +λ
+λ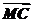 =
=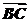 ,
,
即λ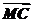 =
=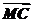 ,∴λ=.
,∴λ=.
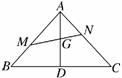 (理)如图,△ABC中,D为BC的中点,G为AD
(理)如图,△ABC中,D为BC的中点,G为AD
的中点,过点G任作一直线MN分别交AB、AC于
M、N两点,若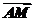 =x
=x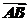 ,
,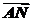 =y
=y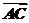 ,求+的值.
,求+的值.
解:设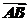 =a,
=a,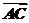 =b,则
=b,则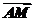 =xa,
=xa,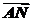 =yb,
=yb,
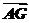 =
=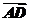 =(
=(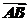 +
+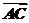 )=(a+b).
)=(a+b).
∴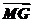 =
=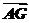 -
-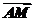 =(a+b)-xa=(-x)a+b,
=(a+b)-xa=(-x)a+b,
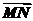 =
=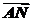 -
-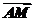 =yb-xa=-xa+yb.
=yb-xa=-xa+yb.
∵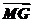 与
与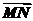 共线,∴存在实数λ,使
共线,∴存在实数λ,使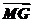 =λ
=λ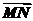 .
.
∴(-x)a+b=λ(-xa+yb)=-λxa+λyb.
∵a与b不共线,∴
消去λ,得+=4,∴+为定值.
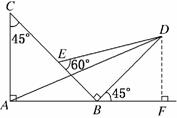
11.(2009·湖南高考)如图,两块斜边长相等的直角三角板拼在一起.若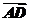 =x
=x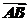 +y
+y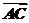 ,则x=________,y=________.
,则x=________,y=________.
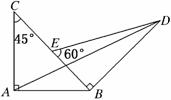
解析:法一:以AB所在直线为x轴,以A为原点建立平面直角坐标系如图,
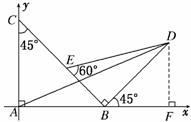
令AB=2.则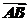 =(2,0),
=(2,0),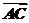 =(0,2),过D作DF⊥AB交AB的延长线为F,
=(0,2),过D作DF⊥AB交AB的延长线为F,
由已知得DF=BF=,
则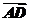 =(2+,).
=(2+,).
∵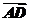 =x
=x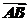 +y
+y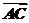 ,∴(2+,)=(2x,2y).
,∴(2+,)=(2x,2y).
即有解得
法二:过D作DF⊥AB交DB的延长线为F.由已知可求得BF=DF=AB,
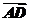 =
= +
+
=(1+)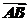 +
+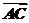 ,
,
所以x=1+,y=.
答案:1+
10.非零不共线向量 、
、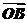 ,且2
,且2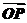 =x
=x +y
+y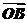 ,若
,若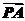 =λ
=λ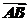 (λ∈R),则点Q(x,y)的轨迹方程是
( )
(λ∈R),则点Q(x,y)的轨迹方程是
( )
A.x+y-2=0 B.2x+y-1=0
C.x+2y-2=0 D.2x+y-2=0
解析: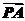 =λ
=λ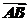 ,得
,得 -
-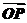 =λ(
=λ(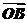 -
- ),
),
即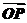 =(1+λ)
=(1+λ)  -λ
-λ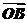 .
.
又2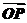 =x
=x +y
+y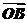 ,
,
∴消去λ得x+y=2.
答案:A
9.已知平面上不共线的四点O、A、B、C.若 -4
-4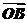 +3
+3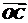 =0,则
=0,则 =________
=________
A. B. C.2 D.3
解析:∵ -4
-4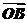 +3
+3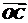 =0,∴(
=0,∴( -
-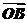 )-3
)-3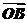 +3
+3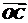 =0,即
=0,即 -
-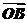 =3(
=3(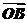 -
-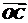 ),∴
),∴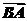 =3
=3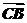 ,∴
,∴ =3.
=3.
答案:D
8.设e1、e2是平面内一组基向量,且a=e1+2e1、b=-e1+e2,则向量e1+e2可以表示另一组基向量a、b的线性组合,则e1+e2=________a+________b.
解析:设e1+e2=xa+yb,
即e1+e2=(x-y)e1+(2x+y)e2.
∴∴x=,y=-.
答案: -
|
题组四 |
向量线性运算的综合应用 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com