
47、(2008浙江21)
已知 是实数,函数
是实数,函数 。
。
(Ⅰ)若 ,求
,求 的值及曲线
的值及曲线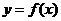 在点
在点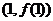 处的切线方程;
处的切线方程;
(Ⅱ)求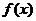 在区间
在区间 上的最大值。
上的最大值。
46、(2008天津21)
设函数 ,其中
,其中 .
.
(Ⅰ)当 时,讨论函数
时,讨论函数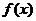 的单调性;
的单调性;
(Ⅱ)若函数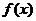 仅在
仅在 处有极值,求
处有极值,求 的取值范围;
的取值范围;
(Ⅲ)若对于任意的 ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求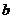 的取值范围.
的取值范围.
45、(2008四川20)
设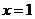 和
和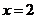 是函数
是函数 的两个极值点。
的两个极值点。
(Ⅰ)求 和
和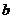 的值;
的值;
(Ⅱ)求 的单调区间
的单调区间
44.(2008山东21)
设函数 ,已知
,已知 和
和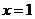 为
为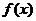 的极值点.
的极值点.
(Ⅰ)求 和
和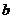 的值;
的值;
(Ⅱ)讨论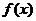 的单调性;
的单调性;
(Ⅲ)设 ,试比较
,试比较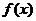 与
与 的大小.
的大小.
43、(全国Ⅱ21)
设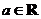 ,函数
,函数 .
.
(Ⅰ)若 是函数
是函数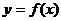 的极值点,求
的极值点,求 的值;
的值;
(Ⅱ)若函数 ,在
,在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.
42、(2008全国Ⅰ21)
已知函数 ,
,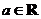 .
.
(Ⅰ)讨论函数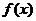 的单调区间;
的单调区间;
(Ⅱ)设函数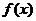 在区间
在区间 内是减函数,求
内是减函数,求 的取值范围.
的取值范围.
41、(2008辽宁22)
设函数 在
在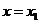 ,
,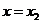 处取得极值,且
处取得极值,且 .
.
(Ⅰ)若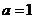 ,求
,求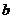 的值,并求
的值,并求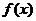 的单调区间;
的单调区间;
(Ⅱ)若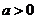 ,求
,求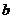 的取值范围.
的取值范围.
40、(2008湖南21)
已知函数 有三个极值点。
有三个极值点。
(I)证明: ;
;
(II)若存在实数c,使函数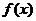 在区间
在区间 上单调递减,求
上单调递减,求 的取值范围。
的取值范围。
39、(2008江西21)
已知函数
(1)求函数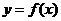 的单调区间;
的单调区间;
(2)若函数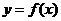 的图像与直线
的图像与直线 恰有两个交点,求
恰有两个交点,求 的取值范围.
的取值范围.
37.(2008福建21)
已知函数 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数y=f(x)的单调区间;
(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
38(2008宁夏21)
设函数 ,曲线
,曲线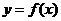 在点
在点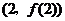 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求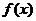 的解析式;
的解析式;
(Ⅱ)证明:曲线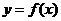 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com