函数不仅是高中数学的核心内容，还是学习高等数学的基础，所以在高考中，函数知识占有极其重要的地位。其试题不但形式多样，而且突出考查学生联系与转化、分类与讨论、数与形结合等重要的数学思想、能力。知识覆盖面广、综合性强、思维力度大、能力要求高，是高考考数学思想、数学方法、考能力、考素质的主阵地

从历年高考形势来看：

(1)与函数图象有关的试题，要从图中(或列表中)读取各种信息，注意利用平移变换、伸缩变换、对称变换，注意函数的对称性、函数值的变化趋势，培养运用数形结合思想来解题的能力，会利用函数图象，进一步研究函数的性质，解决方程、不等式中的问题；

(2)函数综合问题多以知识交汇题为主，甚至以抽象函数为原型来考察；

(3)与幂函数有关的问题主要以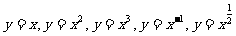为主，利用它们的图象及性质解决实际问题；

预测2010年高考函数图象：(1)题型为1到2个填空选择题；(2)题目多从由解析式得函数图象、数形结合解决问题等方面出题；

函数综合问题：(1)题型为1个大题；(2)题目多以知识交汇题目为主，重在考察函数的工具作用；

幂函数：单独出题的可能性很小，但一些具体问题甚至是一些大题的小过程要应用其性质来解决；

4．通过实例，了解幂函数的概念；结合函数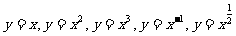的图像，了解它们的变化情况。

3．识图与作图：对于给定的函数图象，能从图象的左右、上下分布范围，变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性、周期性。甚至是处理涉及函数图象与性质一些综合性问题；

2．掌握各种图象变换规则，如：平移变换、对称变换、翻折变换、伸缩变换等；

1．掌握基本初等函数的图象的画法及性质。如正比例函数、反比例函数、一元一次函数、一元二次函数、指数函数、对数函数、幂函数等；

4．运用同角三角函数关系式化简、证明

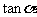　 常用的变形措施有：大角化小，切割化弦等，应用 “弦化切”的技巧，即分子、分母同除以一个不为零的，得到一个只含的教简单的三角函数式。

3．任意角的概念的意义，任意角的三角函数的定义，同角间的三角函数基本关系、诱导公式.由于本重点是任意角的三角函数角的基础，因而三学习本节内容时要注意如下几点：(1)熟练地掌握常用的方法与技巧，在使用三角代换求解有关问题时要注意有关范围的限制；(2)要注意差异分析，又要活用公式，要善于瞄准解题目标进行有效的变形，其解题一般思维模式为：发现差异，寻找联系，合理转化.

只有这样才能在高考中夺得高分。三角函数的值与点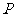在终边上的位置无关，仅与角的大小有关.我们只需计算点到原点的距离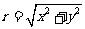,那么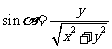,,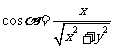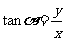。所以，三角函数是以为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数，又因为角的集合与实数集之间可以建立一一对应关系，故三角函数也可以看成实数为自变量的函数.

2．α、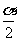、2α之间的关系。

若α终边在第一象限则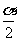终边在第一或第三象限；2α终边在第一或第二象限或y轴正半轴。

若α终边在第二象限则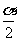终边在第一或第三象限；2α终边在第三或第四象限或y轴负半轴。

若α终边在第三象限则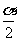终边在第二或第四象限；2α终边在第一或第二象限或y轴正半轴。

若α终边在第四象限则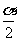终边在第二或第四象限；2α终边在第三或第四象限或y轴负半轴。

1．几种终边在特殊位置时对应角的集合为：

角的终边所在位置	角的集合
X轴正半轴
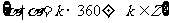Y轴正半轴
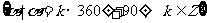X轴负半轴
Y轴负半轴
X轴
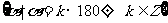Y轴
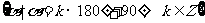坐标轴

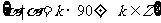12．