(四)用函数方法解题　　　　　　　　　　　　

8、(04年天津)已知数列{a_n},那么“对任意的nN₊,点P_n(n ,a_n)都在直线y=x+1上”是“{a_n}为等差数列”的( B)

A必要条件　 B 充分条件　 C　 充要条件　 D　 既不充分也不必要条件

9、(99年上海)已知等差数列{a_n}满足3a₄=7a₇,且a₁>0,S_n是{a_n}的前n项和，S_n取得最大值，则n=___9______.

10、(01年上海)已知数列{a_n}中a_n=2n-7,(nN₊),++--+=_153___　

(三)用整体化方法解题

5、(00年)已知等差数列{a_n}满足a₁+a₂+a₃+…+a₁₀₁=0,则有(C )　　　　　　　

　 A　 a₁+a₁₀₁>0　　 B　 a₂+a₁₀₀<0　　 C　 a₃+a₉₉=0　　 D　 a₅₁=51

6、(02年)若一个等差数列的前3项和为34，最后3项的和为146，且所有项的和为390，则这个数列的项数为(A)　　　　　　　　　

　　 A　 13　　　　 B　 12　　　　 C 11　　　　　　 D 10

7、(03年上海)在等差数列{a_n}中a₅=3，a₆=-2,a₄+a₅+…+a₁₀=-49

(二)用赋值法解题

2、(96年)等差数列{a_n}的前m项和为30，前2m项和为100，则它的前3m项和为(C )

A　 130　　　　 B　 170　　　 C　 210　　　 D　 260

3、(01年)设{a_n}是公比为q的等比数列， S_n是{a_n}的前n项和,若{S_n}是等差数列，则q=__1_

4、设数列{a_n}的前项的和S_n= (对于所有n1)，且a₄=54,则a₁=__2___

(一)用基本量方法解题

1、(04年浙江)已知等差数列的公差为2，若a_1,a₃,a₄成等比数列，则a₂= (B )

A　 －4　　 B －6　　　 C －8　　　　 D －10　

例1．已知数列{a}是公差d≠0的等差数列，其前n项和为S．

(2)过点Q(1，a)，Q(2，a)作直线12，设l与l的夹角为θ，

证明：(1)因为等差数列{a}的公差d≠0，所以

Kpp是常数(k=2，3，…，n)．

(2)直线l的方程为y-a=d(x-1)，直线l的斜率为d．

例2．已知数列中，是其前项和，并且，

⑴设数列，求证：数列是等比数列；

⑵设数列，求证：数列是等差数列；

⑶求数列的通项公式及前项和。

分析：由于{b}和{c}中的项都和{a}中的项有关，{a}中又有S=4a+2，可由S-S作切入点探索解题的途径．

解：(1)由S=4a，S=4a+2，两式相减，得S-S=4(a-a)，即a=4a-4a．(根据b的构造，如何把该式表示成b与b的关系是证明的关键，注意加强恒等变形能力的训练)

a-2a=2(a-2a)，又b=a-2a，所以b=2b　　 ①

已知S=4a+2，a=1，a+a=4a+2，解得a=5，b=a-2a=3　 ②

由①和②得，数列{b}是首项为3，公比为2的等比数列，故b=3·2．

当n≥2时，S=4a+2=2(3n-4)+2；当n=1时，S=a=1也适合上式．

综上可知，所求的求和公式为S=2(3n-4)+2．

说明：1．本例主要复习用等差、等比数列的定义证明一个数列为等差，等比数列，求数列通项与前项和。解决本题的关键在于由条件得出递推公式。

2．解综合题要总揽全局，尤其要注意上一问的结论可作为下面论证的已知条件，在后面求解的过程中适时应用．

例3．(04年浙江)设数列{a_n}的前项的和S_n=(a_n-1) (n₊),(1)求a_1;a_2; (2)求证数列{a_n}为等比数列。

解: (Ⅰ)由,得 ∴ 又,即,得.

　　 (Ⅱ)当n>1时,

　　 得所以是首项,公比为的等比数列.

例4、(04年重庆)设a₁=1,a₂=,a_n+2=a_n+1-a_n (n=1,2,---),令b_n=a_n+1-a_n (n=1,2---)求数列{b_n}的通项公式，(2)求数列{na_n}的前n项的和S_n。

　　　 解：(I)因

故{b_n}是公比为的等比数列，且

　　　 (II)由

　　　 注意到可得

　　　 记数列的前n项和为T_n，则

例5．在直角坐标平面上有一点列，对一切正整数，点位于函数的图象上，且的横坐标构成以为首项，­为公差的等差数列。

⑴求点的坐标；

⑵设抛物线列中的每一条的对称轴都垂直于轴，第条抛物线的顶点为，且过点，记与抛物线相切于的直线的斜率为，求：。

⑶设，等差数列的任一项，其中是中的最大数，，求的通项公式。

解：(1)

(2)的对称轴垂直于轴，且顶点为.设的方程为：

把代入上式，得，的方程为：。

，

=

(3)，

T中最大数.

设公差为，则，由此得

说明：本例为数列与解析几何的综合题，难度较大(1)、(2)两问运用几何知识算出，解决(3)的关键在于算出及求数列的公差。

例6．数列中，且满足　 　

⑴求数列的通项公式；

⑵设，求；

⑶设=，是否存在最大的整数，使得对任意，均有成立？若存在，求出的值；若不存在，请说明理由。

解：(1)由题意，，为等差数列，设公差为，

由题意得，.

(2)若，

时，

故 　　

(3)

若对任意成立，即对任意成立，

的最小值是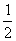，的最大整数值是7。

即存在最大整数使对任意，均有

说明：本例复习数列通项，数列求和以及有关数列与不等式的综合问题。.

5．解综合题的成败在于审清题目，弄懂来龙去脉，透过给定信息的表象，抓住问题的本质，揭示问题的内在联系和隐含条件，明确解题方向，形成解题策略．

4．数列极限的综合题形式多样，解题思路灵活，但万变不离其宗，就是离不开数列极限的概念和性质，离不开数学思想方法，只要能把握这两方面，就会迅速打通解题思路．

3．注意与之间关系的转化。如：

=　 ，　 =．

2．在解决等差数列或等比数列的相关问题时，“基本量法”是常用的方法，但有时灵活地运用性质，可使运算简便，而一般数列的问题常转化为等差、等比数列求解。

1．证明数列是等差或等比数列常用定义，即通过证明 或而得。