
1(汉沽一中2009届月考文17).(本小题满分12分)已知向量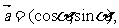
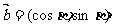 ,
,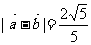 .
.
(1) 求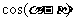 的值;
的值;
(2) 若0<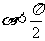 ,
, ,且
,且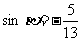 ,求
,求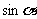 的值.
的值.
解:(1)∵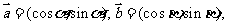
∴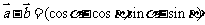 2分
2分
∵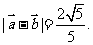 ∴
∴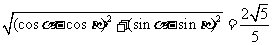 , 2分
, 2分
∴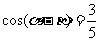 .
6分
.
6分
(2)∵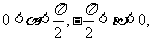 ∴
∴
而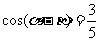 ,∴
,∴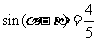 8分
8分
又∵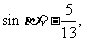 ∴
∴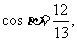 10分
10分
∴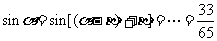 .
12分
.
12分
2 (一中2008-2009月考理17).已知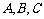 为锐角
为锐角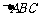 的三个内角,两向量
的三个内角,两向量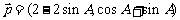 ,
,
 ,若
,若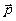 与
与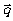 是共线向量.
是共线向量.
(1)求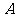 的大小;
的大小;
(2)求函数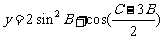 取最大值时,
取最大值时,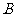 的大小.
的大小.
解:(1)
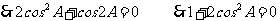

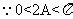 ,
,
(2)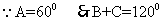
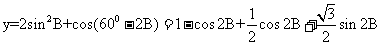
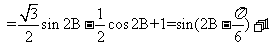
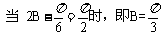
3(2009年滨海新区五所重点学校联考理17).(本题满分12分)在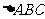 中,
中,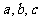 分别
分别
是角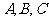 的对边,且
的对边,且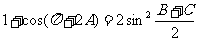 .
.
(Ⅰ)求角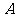 的大小;
的大小;
(Ⅱ)当a=6时,求其面积的最大值,并判断此时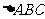 的形状。
的形状。
解: (Ⅰ)由已知得: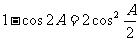 -------------2分
-------------2分
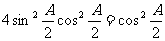
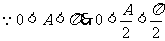
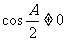 ,
,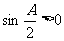
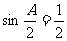 ---------------4分
---------------4分
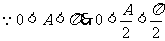
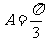 ----------------6分
----------------6分
(Ⅱ) 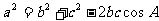
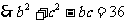 --------------------8分
--------------------8分
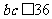
故三角形的面积 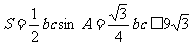 --------------------10分
--------------------10分
当且仅当b=c时等号成立;又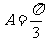 ,故此时
,故此时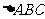 为等边三角形----12分
为等边三角形----12分
4(汉沽一中2008~2009届月考文17)、(本小题满分14分)已知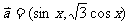 ,
,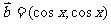 ,
,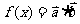
(1)若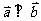 ,求
,求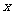 的解集;
的解集;
(2)求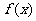 的周期及增区间.
的周期及增区间.
17、解:(1)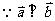 ,
, 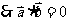 .
.
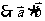
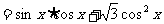 ………………………………………………………2分
………………………………………………………2分
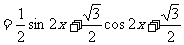 ………………………………………………………4分
………………………………………………………4分
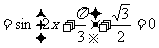 …………………………………6分
…………………………………6分
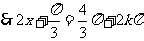 或
或 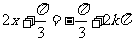
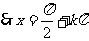 或
或 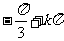
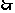 所求解集为
所求解集为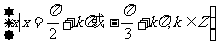 ………………………8分
………………………8分
(2)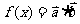
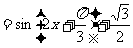
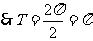 …………………………………………10分
…………………………………………10分
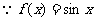 的增区间为
的增区间为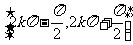
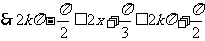 ……………………………………12分
……………………………………12分
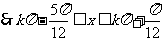
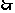 原函数增区间为
原函数增区间为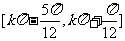
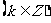 ………………………14分
………………………14分
5(汉沽一中2008~2009届月考理15).(本小题满分12分)
已知向量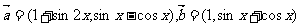 ,设函数
,设函数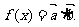
(Ⅰ)求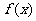 的最大值及相应的
的最大值及相应的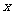 的值;
的值;
(Ⅱ)若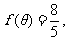 求
求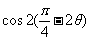 的值.
的值.
解: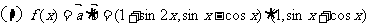
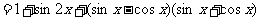 ………………………… 2分
………………………… 2分
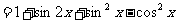
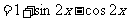 ……………………………………… 4分
……………………………………… 4分
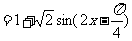 ……………………………………… 6分
……………………………………… 6分
∴当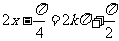 ,即
,即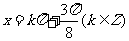 时,
时,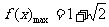 .……… 8分
.……… 8分
(Ⅱ)解法1:由(Ⅰ)知, 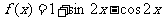
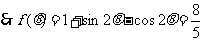 .
.
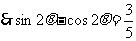 ,两边平方,得
,两边平方,得
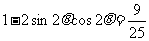 . …… 10分
. …… 10分
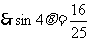 ……………………………… 11分
……………………………… 11分
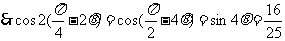 …………………………12分
…………………………12分
解法2:由(Ⅰ)知
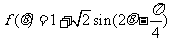
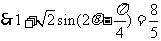
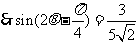 ……………………………… 10分
……………………………… 10分
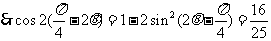 . ………………… 12分
. ………………… 12分
6(汉沽一中2008~2009届月考文18)、(本小题满分14分)
如图,隔河看两目标A、B,但不能到达,在岸边选取相距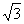 km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
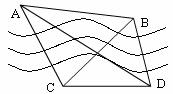
[命题意图]本题主要考查正弦定理和余弦定理以及考查学生的应用意识和解决实际问题的能力.

[解析]在△ACD中,∠ADC=30°,∠ACD=120°,∴∠CAD=30°.
∴AC=CD=3. ……2分
在△BDC中,∠CBD=180°-(45°+75°)=60°. ……3分
由正弦定理,得BC= =
=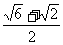 .
……7分
.
……7分
由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠BCA
=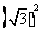 +
+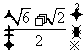 -2
-2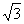 ×
×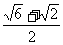 cos75°=5.∴AB=
cos75°=5.∴AB=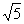 . ……13分
. ……13分
∴两目标A、B之间的距离为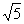 km.
……14分
km.
……14分
7(汉沽一中2008~2009届月考文20)、(本小题满分14分)
已知向量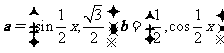 ,
,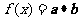
(1)求函数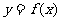 的最小正周期;
的最小正周期;
(2)若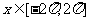 ,求函数
,求函数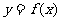 的单调递增区间.
的单调递增区间.
[命题意图]本题平面向量与三角函数的结合,主要考查平面向量的数量积、两角和的三角函数、特殊角的三角函数值、三角函数的周期和求给定范围内的单调区间、不等式的基本性质, 以及考查学生的分析综合能力和转化与化归的数学思想.
[解析]∵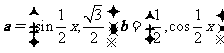
∴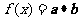
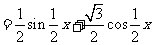 ……2分
……2分
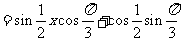 ……3分
……3分
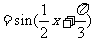 ……5分
……5分
(1) ∵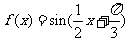 ,∴函数
,∴函数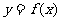 的最小正周期
的最小正周期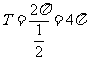 ……7分
……7分
(2)∵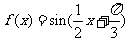 ,令
,令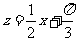 ,函数
,函数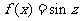 的单调区间是
的单调区间是
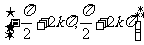 ,
,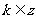 ……8分
……8分
由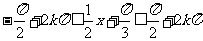 ,
,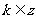
得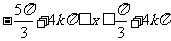 ,
,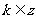 ……11分
……11分
取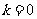 ,得
,得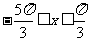 ……12分
……12分
而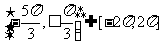 ……13分
……13分
因此,当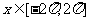 时,函数
时,函数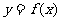 的单调递增区间是
的单调递增区间是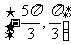 ……14分
……14分
8(和平区2008年高考数学(理)三模17). (本小题满分12分)
已知△ABC的面积S满足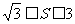 ,且
,且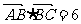 ,
,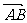 与
与 的夹角为
的夹角为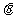 。
。
(1)求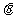 的取值范围;
的取值范围;
(2)求函数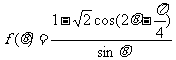 的最大值。
的最大值。
解:(1)∵  (1)(1分)
(1)(1分)
 (2)(3分)
(2)(3分)
由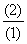 得
得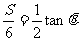 ,即
,即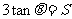
∵ 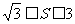 ∴
∴
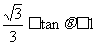
∵ 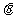 为
为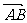 与
与 的夹角 ∴
的夹角 ∴ 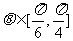 (6分)
(6分)
(2)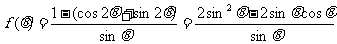
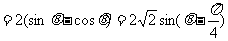 (8分)
(8分)
由于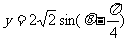 在
在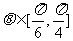 内是增函数(10分)
内是增函数(10分)
∴ 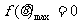 (当且仅当
(当且仅当 时等号成立)(12分)
时等号成立)(12分)
9(武清区2008~2009学年度期中理18)

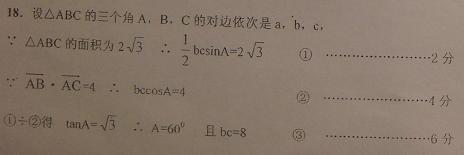

.
1(一中2008-2009月考理15).若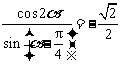 ,则
,则 的值为__
的值为__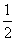 2(2009年滨海新区五所重点学校联考理13).通过观察下述两等式的规律,请你写出一个(包含下面两命题)一般性的命题:
2(2009年滨海新区五所重点学校联考理13).通过观察下述两等式的规律,请你写出一个(包含下面两命题)一般性的命题:
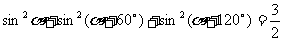
①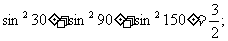
②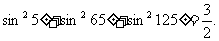
3(汉沽一中2008~2009届月考文13).函数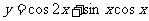 的最小正周期T=__________。13. π
的最小正周期T=__________。13. π
4(汉沽一中2008~2009届月考理9).在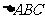 中,
中,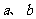 分别为角
分别为角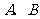 的对边,若
的对边,若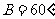 ,
,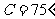 ,
,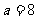 ,则
,则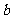 = . 9.
= . 9. 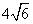 .
.
5(汉沽一中2008~2008学年月考理14).设函数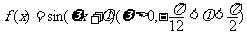 ,给出以下四个论断:
,给出以下四个论断:
①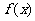 的周期为π; ②
的周期为π; ②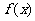 在区间(-
在区间(-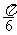 ,0)上是增函数;
,0)上是增函数;
③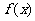 的图象关于点(
的图象关于点(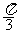 ,0)对称; ④
,0)对称; ④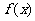 的图象关于直线
的图象关于直线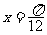 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
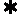 (只需将命题的序号填在横线上).14. ①④
(只需将命题的序号填在横线上).14. ①④ ②③
或 ①③
②③
或 ①③ ②④
②④
6(汉沽一中2009届月考文13).在△ABC中,a,b,c分别是角A,B,C所对的边,已知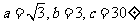 则A=
. 13
则A=
. 13
7(汉沽一中2009届月考文16).有下列命题:①函数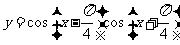 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为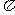 ;②函数
;②函数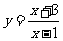 的图象关于点
的图象关于点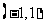 对称;③关于
对称;③关于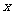 的方程
的方程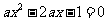 有且仅有一个实数根,则实数
有且仅有一个实数根,则实数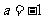 ;④已知命题
;④已知命题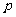 :对任意的
:对任意的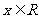 ,都有
,都有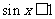 ,则
,则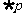 :存在
:存在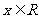 ,使得
,使得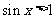 。其中所有真命题的序号是 ③④
。其中所有真命题的序号是 ③④
8(武清区2008~2009学年度期中理)

9(和平区2008年高考数学(文)三模14). 在△ABC中,∠A满足: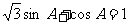 ,AB=2cm,
,AB=2cm,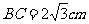 ,则
,则
∠A= 度;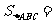
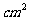 。 14. 120;
。 14. 120;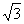
10(和平区2008年高考数学(理)三模13). 在△ABC中,设角A、B、C的对边分别为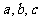 ,且
,且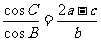 ,则角B= 度。60°
,则角B= 度。60°
1(一中2008-2009月考理)8).函数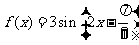 的图象为
的图象为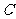 ,
① 图象
,
① 图象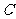 关于直线
关于直线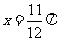 对称;②
函数
对称;②
函数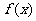 在区间
在区间 内是增函数;③
由
内是增函数;③
由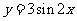 的图象向右平移
的图象向右平移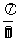 个单位长度可以得到图象
个单位长度可以得到图象 。以上三个论断中,正确论断的个数是
( C )
。以上三个论断中,正确论断的个数是
( C )
A.0 B.1 C.2 D.3 .
2 (2009年滨海新区五所重点学校联考理4). 为得到函数
(2009年滨海新区五所重点学校联考理4). 为得到函数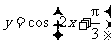 的图像,只需将函数
的图像,只需将函数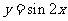 的图像 (4.A )
的图像 (4.A )
A.向左平移 个长度单位 B.向右平移
个长度单位 B.向右平移 个长度单位
个长度单位
C.向左平移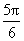 个长度单位 D.向右平移
个长度单位 D.向右平移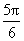 个长度单位
个长度单位
3(汉沽一中2008~2009届月考文5)、下列函数中,在其定义域内既是奇函数又是增函数的是
A.
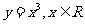 B.
B.
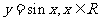
C.
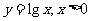 D.
D.
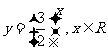
[答案]A
[命题意图]本题主要考查三角函数、对数函数、指数函数、幂函数的基本性质.
[解析] B在其定义域内是奇函数但不是减函数;C是非奇非偶函数;D在其定义域内不是奇函数,是减函数;
4(汉沽一中2008~2009届月考文8)、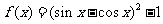 是
是
A.最小正周期为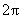 的偶函数 B.最小正周期为
的偶函数 B.最小正周期为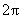 的奇函数
的奇函数
C.最小正周期为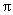 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为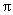 的奇函数
的奇函数
[答案]D
[命题意图]本题主要考查三角函数的平方关系、二倍角公式、周期和奇偶性.
[解析]∵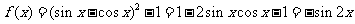
∴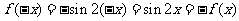 ,
,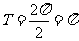 ,故选D
,故选D
5(汉沽一中2008~2008学年月考理4).若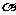 是第二象限的角,且
是第二象限的角,且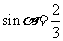 ,则
,则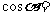 (D)
(D)
A.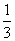 B.
B. 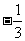 C.
C. 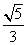 D.
D. 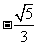
6.(和平区2008年高考数学(理)三模2. 已知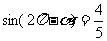 ,
,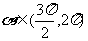 ,则
,则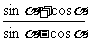 等于(A )
等于(A )
A. 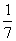 B.
B. 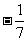 C.
C. 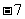 D. 7
D. 7
7(武清区2008~2009学年度期中理) A
A
10.已知M是关于x的不等式2x2+(3a-7)x+3+a-2a2<0解集,且M中的一个元素是0,求实数a的取值范围,并用a表示出该不等式的解集.
原不等式即(2x-a-1)(x+2a-3)<0,
由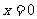 适合不等式故得
适合不等式故得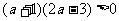 ,所以
,所以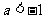 ,或
,或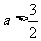 .
.
若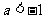 ,则
,则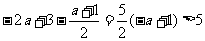 ,∴
,∴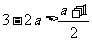 ,
,
此时不等式的解集是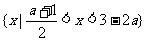 ;
;
若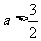 ,由
,由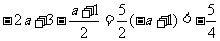 ,∴
,∴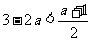 ,
,
此时不等式的解集是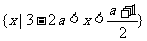 。
。
[探索题]已知f(x)=loga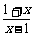 (a>1).
(a>1).
(1)求f(x)在单调区间;
(2)若f(x)≥loga2x,求x的取值范围.
(3)当x∈(r,a-2)时,f(x)的值域为(1,+∞),求a与r的值;
解:(1)由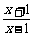 >0得定义域为(-∞,-1)∪(1,+∞)
>0得定义域为(-∞,-1)∪(1,+∞)
∵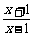 =1+
=1+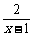 在(1,+∞)上递减,
在(-∞,-1)上也递减,又a>1,
在(1,+∞)上递减,
在(-∞,-1)上也递减,又a>1,
∴f(x)在(-∞,-1),(1,+∞)上是减函数;
(2)由f(x)≥loga2x得
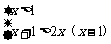

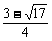 <x<
<x< 且x>1.
且x>1.
∴1<x< .
.
(3)∵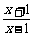 =1+
=1+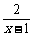 ≠1,∴f(x)≠0.
≠1,∴f(x)≠0.
∵a>1时,x>1 f(x)>0,x<-1
f(x)>0,x<-1 f(x)<0,
f(x)<0,
∴要使f(x)的值域是(1,+∞),只有x>1.
又∵f(x)在(1,+∞)上是减函数,
∴f-1(x)在(1,+∞)上也是减函数.
∴f(x)>1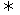 1<x<f-1(1)=
1<x<f-1(1)=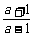 .
.
∴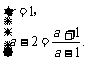 ∴
∴
∴a=2+ ,r=1.
,r=1.
9.解不等式: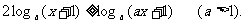
解:原不等式

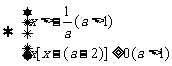
①∴a=2时,不等式的角为x>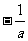 ;
;
②a>2时,a-2>0, 故原不等式解为 <x≤0或x≥a-2
<x≤0或x≥a-2
③当1<a<2时,a-2<0,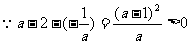
∴原不等式解为 <x≤a-2或x≥0
<x≤a-2或x≥0
8. 己知三个不等式:①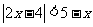
 ②
②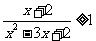 ③
③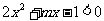
(1)若同时满足①、②的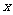 值也满足③,求m的取值范围;
值也满足③,求m的取值范围;
(2)若满足③的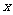 值至少满足①和②中的一个,求m的取值范围。
值至少满足①和②中的一个,求m的取值范围。
分析:本例主要综合复习整式、分式不等式和含绝对值不等式的解法,以及数形结合思想,解本题的关键弄清同时满足①、②的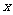 值的满足③的充要条件是:③对应的方程的两根分别在
值的满足③的充要条件是:③对应的方程的两根分别在 和
和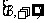 内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。
内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。
解:记①的解集为A,②的解集为B,③的解集为C。
解①得A=(-1,3);解②得B=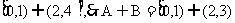
(1) 因同时满足①、②的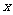 值也满足③,A
值也满足③,A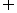 B
B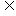 C
C
设 ,由
,由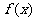 的图象可知:方程的小根小于0,大根大于或等于3时,即可满足
的图象可知:方程的小根小于0,大根大于或等于3时,即可满足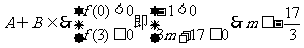
(2) 因满足③的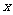 值至少满足①和②中的一个,
值至少满足①和②中的一个,
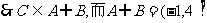 , 因此
, 因此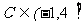
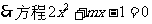 小根大于或等于-1,大根小于或等于4,因而
小根大于或等于-1,大根小于或等于4,因而

说明:同时满足①②的x值满足③的充要条件是:③对应的方程2x +mx-1=0的两根分别在(-∞,0)和[3,+∞)内,因此有f(0)<0且f(3)≤0,否则不能对A∩B中的所有x值满足条件.不等式和与之对应的方程及图象是有着密不可分的内在联系的,在解决问题的过程中,要适时地联系它们之间的内在关系.
+mx-1=0的两根分别在(-∞,0)和[3,+∞)内,因此有f(0)<0且f(3)≤0,否则不能对A∩B中的所有x值满足条件.不等式和与之对应的方程及图象是有着密不可分的内在联系的,在解决问题的过程中,要适时地联系它们之间的内在关系.
7.解不等式:(1)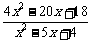 >3.
>3.
(2)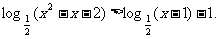
解(1)原不等式可化为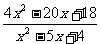 -3>0
-3>0

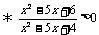
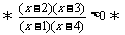
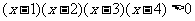
标根作图如下:
∴x∈(-∞,1)∪(2,3)∪(4,+∞).
(2)原不等式变形为
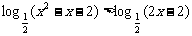 .
.
∴原不等式
 .
.
故原不等式的解集为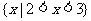
6.由已知a<0,α、β为方程ax2+bx+c=0的两根,
∴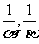 是方程cx2+bx+a=0的根,且
是方程cx2+bx+a=0的根,且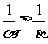
由韦达定理: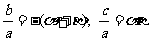 ,
,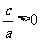 ,a<0得c<0,
,a<0得c<0,
∴不等式cx2+bx+a<0的解集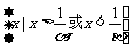 .
.
[解答题]
6.不等式ax2+bx+c>0的解集为{x|α<x<β}其中β>α>0,则不等式cx2+bx+a<0的解集是_____________。
简答.提示:1-3.ACC; 4. 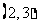 ; 5. 155;
; 5. 155;
5. (2005全国Ⅰ) 若正整数m满足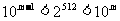 ,则m =
,则m = 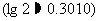
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com