
题型1:直线与椭圆的位置关系
例1.已知椭圆: ,过左焦点F作倾斜角为
,过左焦点F作倾斜角为 的直线交椭圆于A、B两点,求弦AB的长。
的直线交椭圆于A、B两点,求弦AB的长。
解析:a=3,b=1,c=2 ,则F(-2
,则F(-2 ,0)。
,0)。
由题意知: 与
与 联立消去y得:
联立消去y得: 。
。
设A( 、B(
、B( ,则
,则 是上面方程的二实根,由违达定理,
是上面方程的二实根,由违达定理, ,
,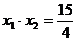 ,
, 又因为A、B、F都是直线
又因为A、B、F都是直线 上的点,
上的点,
所以|AB|=
点评:也可让学生利用“焦半径”公式计算。
例2.中心在原点,一个焦点为F1(0, )的椭圆截直线
)的椭圆截直线 所得弦的中点横坐标为
所得弦的中点横坐标为 ,求椭圆的方程。
,求椭圆的方程。
解析:设椭圆的标准方程为 ,由F1(0,
,由F1(0, )得
)得
把直线方程 代入椭圆方程整理得:
代入椭圆方程整理得: 。
。
设弦的两个端点为 ,则由根与系数的关系得:
,则由根与系数的关系得:
 ,又AB的中点横坐标为
,又AB的中点横坐标为 ,
,
 ,与方程
,与方程 联立可解出
联立可解出
故所求椭圆的方程为: 。
。
点评:根据题意,可设椭圆的标准方程,与直线方程联立解方程组,利用韦达定理及中点坐标公式,求出中点的横坐标,再由F1(0, )知,c=
)知,c= ,
, ,最后解关于a、b的方程组即可。
,最后解关于a、b的方程组即可。
例3.(06辽宁卷)直线 与曲线
与曲线
 的公共点的个数为( )
的公共点的个数为( )
(A)1 (B)2 (C)3 (D)4
解析:将 代入
代入 得:
得: 。
。
 ,显然该关于
,显然该关于 的方程有两正解,即x有四解,所以交点有4个,故选择答案D。
的方程有两正解,即x有四解,所以交点有4个,故选择答案D。
点评:本题考查了方程与曲线的关系以及绝对值的变换技巧,同时对二次方程的实根分布也进行了简单的考查。
例4.(2000上海,17)已知椭圆C的焦点分别为F1( ,0)和F2(2
,0)和F2(2 ,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点,求线段AB的中点坐标。
,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点,求线段AB的中点坐标。
解析:设椭圆C的方程为 ,
,
由题意a=3,c=2 ,于是b=1.
,于是b=1.
∴椭圆C的方程为 +y2=1.
+y2=1.
由 得10x2+36x+27=0,
得10x2+36x+27=0,
因为该二次方程的判别式Δ>0,所以直线与椭圆有两个不同的交点,
设A(x1,y1),B(x2,y2),
则x1+x2= ,
,
故线段AB的中点坐标为( ).
).
点评:本题主要考查椭圆的定义标准方程,直线与椭圆的位置关系及线段中点坐标公式。
题型2:直线与双曲线的位置关系
例5.(1)过点 与双曲线
与双曲线 有且只有一个公共点的直线有几条,分别求出它们的方程。
有且只有一个公共点的直线有几条,分别求出它们的方程。
(2)直线 与双曲线
与双曲线 相交于A、B两点,当
相交于A、B两点,当 为何值时,A、B在双曲线的同一支上?当
为何值时,A、B在双曲线的同一支上?当 为何值时,A、B分别在双曲线的两支上?
为何值时,A、B分别在双曲线的两支上?
解析:(1)解:若直线的斜率不存在时,则 ,此时仅有一个交点
,此时仅有一个交点 ,满足条件;
,满足条件;
若直线的斜率存在时,设直线的方程为 则
则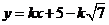 ,
,
 , ∴
, ∴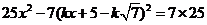 ,
,
 ,
,
当 时,方程无解,不满足条件;
时,方程无解,不满足条件;
当 时,
时, 方程有一解,满足条件;
方程有一解,满足条件;
当 时,令
时,令 ,
,
化简得: 无解,所以不满足条件;
无解,所以不满足条件;
所以满足条件的直线有两条 和
和 。
。
(2)把 代入
代入 整理得:
整理得: ……(1)
……(1)
当 时,
时, 。
。
由 >0得
>0得 且
且 时,方程组有两解,直线与双曲线有两个交点。
时,方程组有两解,直线与双曲线有两个交点。
若A、B在双曲线的同一支,须 >0 ,所以
>0 ,所以 或
或 。
。
故当 或
或 时,A、B两点在同一支上;当
时,A、B两点在同一支上;当 时,A、B两点在双曲线的两支上。
时,A、B两点在双曲线的两支上。
点评:与双曲线只有一个公共点的直线有两种。一种是与渐近线平行的两条与双曲线交于一点的直线。另一种是与双曲线相切的直线也有两条。
例5.(1)求直线 被双曲线
被双曲线 截得的弦长;
截得的弦长;
(2)求过定点 的直线被双曲线
的直线被双曲线 截得的弦中点轨迹方程。
截得的弦中点轨迹方程。
解析:由
 得
得 得
得 (*)
(*)
设方程(*)的解为 ,则有
,则有 得,
得,

(2)方法一:若该直线的斜率不存在时与双曲线无交点,则设直线的方程为 ,它被双曲线截得的弦为
,它被双曲线截得的弦为 对应的中点为
对应的中点为 ,
,
由 得
得 (*)
(*)
设方程(*)的解为 ,则
,则 ,
,
∴ ,
,
且 ,
,
∴ ,
,

得 或
或 。
。
方法二:设弦的两个端点坐标为 ,弦中点为
,弦中点为 ,则
,则
 得:
得: ,
,
∴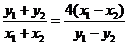 , 即
, 即 , 即
, 即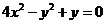 (图象的一部分)
(图象的一部分)
点评:(1)弦长公式 ;(2)有关中点弦问题的两种处理方法。
;(2)有关中点弦问题的两种处理方法。
例7.过双曲线的一焦点的直线垂直于一渐近线,且与双曲线的两支相交,求该双曲线离心率的范围。
解析:设双曲线的方程为 ,
, ,渐近线
,渐近线 ,则过
,则过 的直线方程为
的直线方程为 ,则
,则 ,
,
代入得 ,
,
∴ 即得
即得 ,
,
∴ ,即得到
,即得到 。
。
点评:直线与圆锥曲线的位置关系经常和圆锥曲线的几何要素建立起对应关系,取值范围往往与判别式的取值建立联系。
题型3:直线与抛物线的位置关系
例8.已知抛物线方程为 ,直线
,直线 过抛物线的焦点F且被抛物线截得的弦长为3,求p的值。
过抛物线的焦点F且被抛物线截得的弦长为3,求p的值。
解析:设 与抛物线交于
与抛物线交于
由距离公式|AB|= =
=
由

从而 由于p>0,解得
由于p>0,解得
点评:方程组有两组不同实数解或一组实数解则相交;有两组相同实数解则相切;无实数解则相离。
例9.2003上海春,4)直线y=x-1被抛物线y2=4x截得线段的中点坐标是_____.
答案:(3,2)
解法一:设直线y=x-1与抛物线y2=4x交于A(x1,y1),B(x2,y2),其中点为P(x0,y0)。
由题意得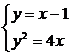 ,(x-1)2=4x,x2-6x+1=0。
,(x-1)2=4x,x2-6x+1=0。
∴x0= =3.y0=x0-1=2.∴P(3,2)。
=3.y0=x0-1=2.∴P(3,2)。
解法二:y22=4x2,y12=4x1,y22-y12=4x2-4x1,
 =4.∴y1+y2=4,即y0=2,x0=y0+1=3。
=4.∴y1+y2=4,即y0=2,x0=y0+1=3。
故中点为P(3,2)。
点评:本题考查曲线的交点与方程的根的关系.同时应注意解法一中的纵坐标与解法二中的横坐标的求法。
例10.(1997上海)抛物线方程为y2=p(x+1)(p>0),直线x+y=m与x轴的交点在抛物线的准线的右边.
(1)求证:直线与抛物线总有两个交点;
(2)设直线与抛物线的交点为Q、R,OQ⊥OR,求p关于m的函数f(m)的表达式;
(3)(文)在(2)的条件下,若抛物线焦点F到直线x+y=m的距离为 ,求此直线的方程;
,求此直线的方程;
(理)在(2)的条件下,若m变化,使得原点O到直线QR的距离不大于 ,求p的值的范围.
,求p的值的范围.
解:(1)抛物线y2=p(x+1)的准线方程是x=-1- ,直线x+y=m与x轴的交点为(m,0),由题设交点在准线右边,得m>-1-
,直线x+y=m与x轴的交点为(m,0),由题设交点在准线右边,得m>-1- ,即4m+p+4>0.
,即4m+p+4>0.
由
得x2-(2m+p)x+(m2-p)=0.
而判别式Δ=(2m+p)2-4(m2-p)=p(4m+p+4).
又p>0及4m+p+4>0,可知Δ>0.
因此,直线与抛物线总有两个交点;
(2)设Q、R两点的坐标分别为(x1,y1)、(x2,y2),由(1)知,x1、x2是方程x2-(2m+p)x+m2-p=0的两根,
∴x1+x2=2m+p,x1·x2=m2-p.
由OQ⊥OR,得kOQ·kOR=-1,
即有x1x2+y1y2=0.
又Q、R为直线x+y=m上的点,
因而y1=-x1+m,y2=-x2+m.
于是x1x2+y1y2=2x1x2-m(x1+x2)+m2=2(m2-p)-m(2m+p)+m2=0,
∴p=f(m)= ,
,
由 得m>-2,m≠0;
得m>-2,m≠0;
(3)(文)由于抛物线y2=p(x+1)的焦点F坐标为(-1+ ,0),于是有
,0),于是有
 ,即|p-4m-4|=4.
,即|p-4m-4|=4.
又p= ∴|
∴| |=4.
|=4.
解得m1=0,m2=- ,m3=-4,m4=-
,m3=-4,m4=- .
.
但m≠0且m>-2,因而舍去m1、m2、m3,故所求直线方程为3x+3y+4=0.
(理)解法一:由于原点O到直线x+y=m的距离不大于 ,于是
,于是
 ,∴|m|≤1.
,∴|m|≤1.
由(2),知m>-2且m≠0,
故m∈[-1,0)∪(0,1].
由(2),知f(m)= =(m+2)+
=(m+2)+ -4,
-4,
当m∈[-1,0)时,任取m1、m2,0>m1>m2≥-1,则
f(m1)-f(m2)=(m1-m2)+( )
)
=(m1-m2)[1- ].
].
由0>m1>m2≥-1,知0<(m1+2)(m2+2)<4,1- <0.
<0.
又由m1-m2>0知f(m1)<f(m2)因而f(m)为减函数.
可见,当m∈[-1,0)时,p∈(0,1].
同样可证,当m∈(0,1]时,f(m)为增函数,从而p∈(0, ].
].
解法二:由解法一知,m∈[-1,0)∪(0,1].由(2)知
p=f(m)= .
.
设t= ,g(t)=t+2t2,则t∈(-∞,-1]∪[1,+∞),又
,g(t)=t+2t2,则t∈(-∞,-1]∪[1,+∞),又
g(t)=2t2+t=2(t+ )2-
)2- .
.
∴当t∈(-∞,-1]时,g(t)为减函数,g(t)∈[1,+∞).
当t∈[1,+∞)时,g(t)为增函数,g(t)∈[3,+∞).
因此,当m∈[-1,0]时,t∈(-∞,-1],p= ∈(0,1];
∈(0,1];
当m∈(0,1]时,t∈[1,+∞),p∈(0, ].
].
点评:本题考查抛物线的性质与方程,抛物线与直线的位置关系,点到直线的距离,函数与不等式的知识,以及解决综合问题的能力。
例11.(06山东卷)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是 。
解析:显然 ³0,又
³0,又 =4(
=4( )³8
)³8 ,当且仅当
,当且仅当 时取等号,所以所求的值为32。
时取等号,所以所求的值为32。
点评:该题考查直线与抛物线位置关系下的部分求值问题,结合基本不等式求得最终结果。
3.直线与圆锥曲线相交的弦长公式
设直线l:y=kx+n,圆锥曲线:F(x,y)=0,它们的交点为P1 (x1,y1),P2 (x2,y2),
且由 ,消去y→ax2+bx+c=0(a≠0),Δ=b2 -4ac。
,消去y→ax2+bx+c=0(a≠0),Δ=b2 -4ac。
则弦长公式为:
d= =
= =
= =
= 。
。
焦点弦长: (点
(点 是圆锥曲线上的任意一点,
是圆锥曲线上的任意一点, 是焦点,
是焦点, 是
是 到相应于焦点
到相应于焦点 的准线的距离,
的准线的距离, 是离心率)。
是离心率)。
2.直线与圆锥曲线的位置关系
直线与圆锥曲线的位置关系,从几何角度可分为三类:无公共点,仅有一个公共点及有两个相异公共点。
直线与圆锥曲线的位置关系的研究方法可通过代数方法即解方程组的办法来研究。因为方程组解的个数与交点的个数是一样的。
直线与圆锥曲线的位置关系可分为:相交、相切、相离.对于抛物线来说,平行于对称轴的直线与抛物线相交于一点,但并不是相切;对于双曲线来说,平行于渐近线的直线与双曲线只有一个交点,但并不相切.这三种位置关系的判定条件可引导学生归纳为:



注意:直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件,但不是充分条件.
1.点M(x0,y0)与圆锥曲线C:f(x,y)=0的位置关系

2.与直线、圆锥曲线相结合的综合型考题,等轴双曲线基本不出题,坐标轴平移或平移化简方程一般不出解答题,大多是以选择题形式出现。
近几年来直线与圆锥曲线的位置关系在高考中占据高考解答题压轴题的位置,且选择、填空也有涉及,有关直线与圆锥曲线的位置关系的题目可能会涉及线段中点、弦长等。分析这类问题,往往利用数形结合的思想和“设而不求”的方法,对称的方法及韦达定理等。
预测07年高考:
1.会出现1道关于直线与圆锥曲线的位置关系的解答题;
2.掌握直线与圆锥曲线的位置关系判定及其相关问题。
1.通过圆锥曲线与方程的学习,进一步体会数形结合的思想;
在复习过程中抓住以下几点:
(1)坚持源于课本、高于课本,以考纲为纲的原则。高考命题的依据是《高考说明》.并明确考点及对知识点与能力的要求作出了明确规定,其实质是精通课本,而本章考题大多数是课本的变式题,即源于课本,因此掌握双基、精通课本是关键;
(2)在注重解题方法、数学思想的应用的同时注意一些解题技巧,椭圆、双曲线、抛物线的定义揭示了各自存在的条件、性质及几何特征与圆锥曲线的焦点、焦半径、准线、离心率有关量的关系问题,若能用定义法,可避免繁琐的推理与运算;
(3)焦半径公式:抛物线上一点P(x1,y1),F为抛物线的焦点,对于四种抛物线的焦半径公式分别为(p>0):

题型1:椭圆的概念及标准方程
例1.求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是 、
、 ,椭圆上一点
,椭圆上一点 到两焦点距离的和等于
到两焦点距离的和等于 ;
;
(2)两个焦点的坐标分别是 、
、 ,并且椭圆经过点
,并且椭圆经过点 ;
;
(3)焦点在 轴上,
轴上, ,
, ;
;
(4)焦点在 轴上,
轴上, ,且过点
,且过点 ;
;
(5)焦距为 ,
, ;
;
(6)椭圆经过两点 ,
, 。
。
解析:(1)∵椭圆的焦点在 轴上,故设椭圆的标准方程为
轴上,故设椭圆的标准方程为 (
( ),
),
∵ ,
,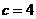 ,∴
,∴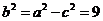 ,
,
所以,椭圆的标准方程为 。
。
(2)∵椭圆焦点在 轴上,故设椭圆的标准方程为
轴上,故设椭圆的标准方程为 (
( ),
),
由椭圆的定义知,
 ,
,
∴ ,又∵
,又∵ ,∴
,∴ ,
,
所以,椭圆的标准方程为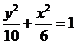 。
。
(3)∵ ,∴
,∴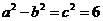 ,①
,①
又由 代入①得
代入①得 ,
,
∴ ,∴
,∴ ,又∵焦点在
,又∵焦点在 轴上,
轴上,
所以,椭圆的标准方程为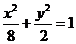 。
。
(4)设椭圆方程为 ,
,
∴ ,∴
,∴ ,
,
又∵ ,∴
,∴ ,
,
所以,椭圆的标准方程为 .
.
(5)∵焦距为 ,∴
,∴ ,
,
∴ ,又∵
,又∵ ,∴
,∴ ,
, ,
,
所以,椭圆的标准方程为 或
或 .
.
(6)设椭圆方程为 (
( ),
),
由 得
得 ,
,
所以,椭圆方程为 .
.
点评:求椭圆的方程首先清楚椭圆的定义,还要知道椭圆中一些几何要素与椭圆方程间的关系。
例2.(1)(06山东)已知椭圆中心在原点,一个焦点为F(-2 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
(2)(06天津理,8)椭圆的中心为点 ,它的一个焦点为
,它的一个焦点为 ,相应于焦点
,相应于焦点 的准线方程为
的准线方程为 ,则这个椭圆的方程是( )
,则这个椭圆的方程是( )
A. B.
B.
C. D.
D.
解析:(1)已知 为所求;
为所求;
(2)椭圆的中心为点 它的一个焦点为
它的一个焦点为
∴ 半焦距 ,相应于焦点F的准线方程为
,相应于焦点F的准线方程为
∴  ,
, ,则这个椭圆的方程是
,则这个椭圆的方程是 ,选D。
,选D。
点评:求椭圆方程的题目属于中低档题目,掌握好基础知识就可以。
题型2:椭圆的性质
例3.(1)(06山东理,7)在给定椭圆中,过焦点且垂直于长轴的弦长为 ,焦点到相应准线的距离为1,则该椭圆的离心率为( )
,焦点到相应准线的距离为1,则该椭圆的离心率为( )
(A) (B)
(B) (C)
(C)  (D)
(D)
(2)(1999全国,15)设椭圆 =1(a>b>0)的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦的长等于点F1到l1的距离,则椭圆的离心率是
。
=1(a>b>0)的右焦点为F1,右准线为l1,若过F1且垂直于x轴的弦的长等于点F1到l1的距离,则椭圆的离心率是
。
解析:(1)不妨设椭圆方程为 (a>b>0),则有
(a>b>0),则有 ,据此求出e=
,据此求出e= ,选B。
,选B。
(2) ;解析:由题意知过F1且垂直于x轴的弦长为
;解析:由题意知过F1且垂直于x轴的弦长为 ,
,
∴ ,∴
,∴ ,∴
,∴ ,即e=
,即e= 。
。
点评:本题重点考查了椭圆的基本性质。
例4.(1)(2000京皖春,9)椭圆短轴长是2,长轴是短轴的2倍,则椭圆中心到其准线距离是( )
A. B.
B. C.
C. D.
D.
(2)(1998全国理,2)椭圆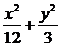 =1的焦点为F1和F2,点P在椭圆上.如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1和F2,点P在椭圆上.如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
A.7倍 B.5倍 C.4倍 D.3倍
解析:(1)D;由题意知a=2,b=1,c= ,准线方程为x=±
,准线方程为x=± ,
,
∴椭圆中心到准线距离为 .
.
(2)A;不妨设F1(-3,0),F2(3,0)由条件得P(3,± ),即|PF2|=
),即|PF2|= ,|PF1|=
,|PF1|= ,因此|PF1|=7|PF2|,故选A。
,因此|PF1|=7|PF2|,故选A。
点评:本题主要考查椭圆的定义及数形结合思想,具有较强的思辨性,是高考命题的方向。
题型3:双曲线的方程
例5.(1)已知焦点 ,双曲线上的一点
,双曲线上的一点 到
到 的距离差的绝对值等于
的距离差的绝对值等于 ,求双曲线的标准方程;
,求双曲线的标准方程;
(2)求与椭圆 共焦点且过点
共焦点且过点 的双曲线的方程;
的双曲线的方程;
(3)已知双曲线的焦点在 轴上,并且双曲线上两点
轴上,并且双曲线上两点 坐标分别为
坐标分别为 ,求双曲线的标准方程。
,求双曲线的标准方程。
解析:(1)因为双曲线的焦点在 轴上,所以设它的标准方程为
轴上,所以设它的标准方程为
 ,
,
∵ ,∴
,∴ ,∴
,∴ 。
。
所以所求双曲线的方程为 ;
;
(2)椭圆 的焦点为
的焦点为 ,可以设双曲线的方程为
,可以设双曲线的方程为 ,则
,则 。
。
又∵过点 ,∴
,∴ 。
。
综上得, ,所以
,所以 。
。
点评:双曲线的定义;方程确定焦点的方法;基本量 之间的关系。
之间的关系。
(3)因为双曲线的焦点在 轴上,所以设所求双曲线的标准方程为
轴上,所以设所求双曲线的标准方程为 ①;
①;
∵点 在双曲线上,∴点
在双曲线上,∴点 的坐标适合方程①。
的坐标适合方程①。
将 分别代入方程①中,得方程组:
分别代入方程①中,得方程组:
将 和
和 看着整体,解得
看着整体,解得 ,
,
∴ 即双曲线的标准方程为
即双曲线的标准方程为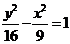 。
。
点评:本题只要解得 即可得到双曲线的方程,没有必要求出
即可得到双曲线的方程,没有必要求出 的值;在求解的过程中也可以用换元思想,可能会看的更清楚。
的值;在求解的过程中也可以用换元思想,可能会看的更清楚。
例6.(06上海卷)已知双曲线中心在原点,一个顶点的坐标为 ,且焦距与虚轴长之比为
,且焦距与虚轴长之比为 ,则双曲线的标准方程是____________________.
,则双曲线的标准方程是____________________.
解析:双曲线中心在原点,一个顶点的坐标为 ,则焦点在x轴上,且a=3,焦距与虚轴长之比为
,则焦点在x轴上,且a=3,焦距与虚轴长之比为 ,即
,即 ,解得
,解得 ,则双曲线的标准方程是
,则双曲线的标准方程是 ;
;
点评:本题主要考查双曲线的基础知识以及综合运用知识解决问题的能力。充分挖掘双曲线几何性质,数形结合,更为直观简捷。
题型4:双曲线的性质
例7.(1)(06福建卷)已知双曲线 (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A.( 1,2) B. (1,2) C.[2,+∞] D.(2,+∞)
(2)(06湖南卷)过双曲线M: 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线 ,若
,若 与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是 ( )
与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是 ( )
A. B.
B. C.
C. D.
D.
(3)(06陕西卷)已知双曲线 - =1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A.2 B. C. D.
解析:(1)双曲线 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为 的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率
的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率 ,
,
∴  ≥
≥ ,离心率e2=
,离心率e2= ,∴ e≥2,选C。
,∴ e≥2,选C。
(2)过双曲线 的左顶点
的左顶点 (1,0)作斜率为1的直线
(1,0)作斜率为1的直线 :y=x-1,
若
:y=x-1,
若 与双曲线
与双曲线 的两条渐近线
的两条渐近线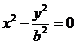 分别相交于点
分别相交于点 , 联立方程组代入消元得
, 联立方程组代入消元得 ,
,
∴  ,x1+x2=2x1x2,
,x1+x2=2x1x2,
又 ,则B为AC中点,2x1=1+x2,代入解得
,则B为AC中点,2x1=1+x2,代入解得 ,
,
∴
b2=9,双曲线 的离心率e=
的离心率e= ,选A。
,选A。
(3)双曲线 (a>)的两条渐近线的夹角为,则
(a>)的两条渐近线的夹角为,则 ,∴ a2=6,双曲线的离心率为 ,选D。
,∴ a2=6,双曲线的离心率为 ,选D。
点评:高考题以离心率为考察点的题目较多,主要实现 三元素之间的关系。
三元素之间的关系。
例8.(1)(06江西卷)P是双曲线 的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
A. 6 B.7 C.8 D.9
(2)(06全国卷I)双曲线 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则
A. B.
B. C.
C. D.
D.
(3)(06天津卷)如果双曲线的两个焦点分别为 、
、 ,一条渐近线方程为
,一条渐近线方程为 ,那么它的两条准线间的距离是( )
,那么它的两条准线间的距离是( )
A. B.
B. C.
C. D.
D.
解析:(1)设双曲线的两个焦点分别是F1(-5,0)与F2(5,0),则这两点正好是两圆的圆心,当且仅当点P与M、F1三点共线以及P与N、F2三点共线时所求的值最大,此时|PM|-|PN|=(|PF1|-2)-(|PF2|-1)=10-1=9故选B。
(2)双曲线 的虚轴长是实轴长的2倍,∴ m<0,且双曲线方程为
的虚轴长是实轴长的2倍,∴ m<0,且双曲线方程为 ,∴ m=
,∴ m= ,选A。
,选A。
(3)如果双曲线的两个焦点分别为 、
、 ,一条渐近线方程为
,一条渐近线方程为 ,
,
∴ 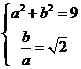 ,解得
,解得 ,所以它的两条准线间的距离是
,所以它的两条准线间的距离是 ,选C。
,选C。
点评:关于双曲线渐近线、准线及许多距离问题也是考察的重点。
题型5:抛物线方程
例9.(1))焦点到准线的距离是2;
(2)已知抛物线的焦点坐标是F(0, 2),求它的标准方程。
2),求它的标准方程。
解析:(1)y =4x,y
=4x,y =
= 4x,x
4x,x =4y,x
=4y,x =
= 4y;
4y;

方程是x =
= 8y。
8y。
点评:由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程。当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解。
题型6:抛物线的性质
例10.(1)(06安徽卷)若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. B.
B. C.
C. D.
D.
(2)(浙江卷)抛物线 的准线方程是(
)
的准线方程是(
)
(A)  (B)
(B)  (C)
(C)  (D)
(D)

(3)(06上海春)抛物线 的焦点坐标为( )
的焦点坐标为( )
(A) . (B)
. (B) . (C)
. (C) . (D)
. (D)
解析:(1)椭圆 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线 的焦点为(2,0),则
的焦点为(2,0),则 ,故选D;
,故选D;
(2)2p=8,p=4,故准线方程为x=-2,选A;
(3)(直接计算法)因为p=2
,所以抛物线y2=4x的焦点坐标为  。应选B。
。应选B。
点评:考察抛物线几何要素如焦点坐标、准线方程的题目根据定义直接计算机即可。
例11.(1)(全国卷I)抛物线 上的点到直线
上的点到直线 距离的最小值是( )
距离的最小值是( )
A. B.
B. C.
C. D.
D.
(2)(2002全国文,16)对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的通径的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。
(3)(2001广东、河南,10)对于抛物线y2=4x上任意一点Q,点P(a,0)都满足|PQ|≥|a|,则a的取值范围是( )
A.(-∞,0) B.(-∞,2 C.[0,2] D.(0,2)
C.[0,2] D.(0,2)
能使这抛物线方程为y2=10x的条件是 .(要求填写合适条件的序号)
解析:(1)设抛物线 上一点为(m,-m2),该点到直线
上一点为(m,-m2),该点到直线 的距离为
的距离为 ,当m=
,当m= 时,取得最小值为
时,取得最小值为 ,选A;
,选A;
(2)答案:②,⑤
解析:从抛物线方程易得②,分别按条件③、④、⑤计算求抛物线方程,从而确定⑤。
(3)答案:B
解析:设点Q的坐标为( ,y0),
,y0),
由 |PQ|≥|a|,得y02+( -a)2≥a2.
-a)2≥a2.
整理,得:y02(y02+16-8a)≥0,
∵y02≥0,∴y02+16-8a≥0.
即a≤2+ 恒成立.而2+
恒成立.而2+ 的最小值为2.
的最小值为2.
∴a≤2.选B。
点评:抛物线问题多考察一些距离、最值及范围问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com