
1.方程 的解集为( )
的解集为( )
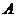 .
.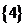
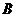 .
.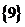
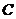 .
.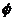
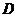 .
.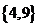
例1.一个口袋内装有大小不同的7个白球和1个黑球,
(1)从口袋内取出3个球,共有多少种取法?
(2)从口袋内取出3个球,使其中含有1个黑球,有多少种取法?
(3)从口袋内取出3个球,使其中不含黑球,有多少种取法?
解:(1)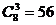 ,或
,或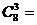
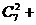
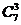 ,;(2)
,;(2)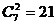 ;(3)
;(3)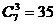 .
.
例2.(1)计算: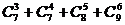 ;
;
(2)求证: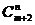 =
=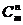 +
+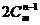 +
+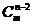 .
.
解:(1)原式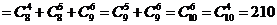 ;
;
证明:(2)右边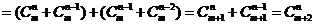
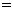 左边
左边
例3.解方程:(1)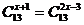 ;(2)解方程:
;(2)解方程: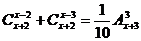 .
.
解:(1)由原方程得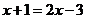 或
或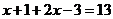 ,∴
,∴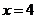 或
或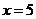 ,
,
又由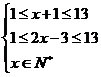 得
得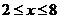 且
且 ,∴原方程的解为
,∴原方程的解为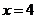 或
或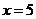

上述求解过程中的不等式组可以不解,直接把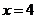 和
和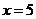 代入检验,这样运算量小得多.
代入检验,这样运算量小得多.
(2)原方程可化为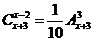 ,即
,即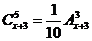 ,∴
,∴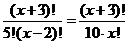 ,
,
∴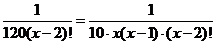 ,
,
∴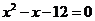 ,解得
,解得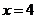 或
或 ,
,
经检验: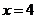 是原方程的解
是原方程的解 
1 组合数的性质1:
组合数的性质1: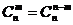 .
.
一般地,从n个不同元素中取出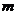 个元素后,剩下
个元素后,剩下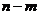 个元素.因为从n个不同元素中取出m个元素的每一个组合,与剩下的n - m个元素的每一个组合一一对应,所以从n个不同元素中取出m个元素的组合数,等于从这n个元素中取出n - m个元素的组合数,即:
个元素.因为从n个不同元素中取出m个元素的每一个组合,与剩下的n - m个元素的每一个组合一一对应,所以从n个不同元素中取出m个元素的组合数,等于从这n个元素中取出n - m个元素的组合数,即: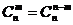 .在这里,主要体现:“取法”与“剩法”是“一一对应”的思想
.在这里,主要体现:“取法”与“剩法”是“一一对应”的思想
证明:∵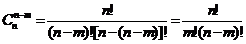
又 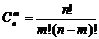 ,∴
,∴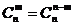

说明:①规定: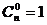 ;
;
②等式特点:等式两边下标同,上标之和等于下标;
③此性质作用:当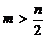 时,计算
时,计算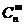 可变为计算
可变为计算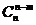 ,能够使运算简化.
,能够使运算简化.
例如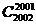 =
=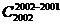 =
=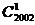 =2002;
=2002;
④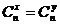
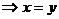 或
或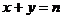 .
.
2.组合数的性质2: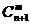 =
=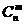 +
+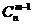 .
.
一般地,从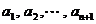 这n+1个不同元素中取出m个元素的组合数是
这n+1个不同元素中取出m个元素的组合数是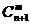 ,这些组合可以分为两类:一类含有元素
,这些组合可以分为两类:一类含有元素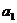 ,一类不含有
,一类不含有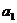 .含有
.含有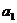 的组合是从
的组合是从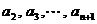 这n个元素中取出m -1个元素与
这n个元素中取出m -1个元素与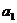 组成的,共有
组成的,共有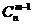 个;不含有
个;不含有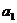 的组合是从
的组合是从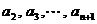 这n个元素中取出m个元素组成的,共有
这n个元素中取出m个元素组成的,共有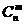 个.根据分类计数原理,可以得到组合数的另一个性质.在这里,主要体现从特殊到一般的归纳思想,“含与不含其元素”的分类思想.
个.根据分类计数原理,可以得到组合数的另一个性质.在这里,主要体现从特殊到一般的归纳思想,“含与不含其元素”的分类思想.
证明: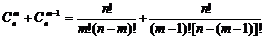
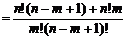
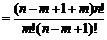
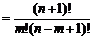
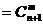
∴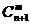 =
=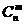 +
+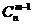 .
.
说明:①公式特征:下标相同而上标差1的两个组合数之和,等于下标比原下标多1而上标与大的相同的一个组合数;
②此性质的作用:恒等变形,简化运算 
10.组合数公式:
或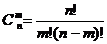
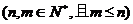


9.组合数的概念:从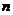 个不同元素中取出
个不同元素中取出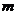
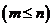 个元素的所有组合的个数,叫做从
个元素的所有组合的个数,叫做从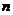 个不同元素中取出
个不同元素中取出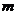 个元素的组合数.用符号
个元素的组合数.用符号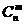 表示.
表示.
7.排列数的另一个计算公式: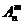 =
=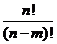


8 组合的概念:一般地,从
组合的概念:一般地,从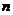 个不同元素中取出
个不同元素中取出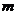
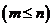 个元素并成一组,叫做从
个元素并成一组,叫做从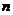 个不同元素中取出
个不同元素中取出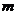 个元素的一个组合
个元素的一个组合
说明:⑴不同元素;⑵“只取不排”--无序性;⑶相同组合:元素相同
5.排列数公式: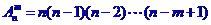 (
(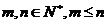 )
)
6 阶乘:
阶乘: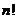 表示正整数1到
表示正整数1到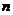 的连乘积,叫做
的连乘积,叫做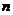 的阶乘
的阶乘 规定
规定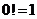 .
.
4.排列数的定义:从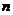 个不同元素中,任取
个不同元素中,任取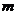 (
( )个元素的所有排列的个数叫做从
)个元素的所有排列的个数叫做从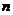 个元素中取出
个元素中取出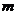 元素的排列数,用符号
元素的排列数,用符号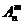 表示
表示
3.排列的概念:从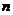 个不同元素中,任取
个不同元素中,任取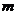 (
( )个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从
)个元素(这里的被取元素各不相同)按照一定的顺序排成一列,叫做从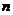 个不同元素中取出
个不同元素中取出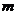 个元素的一个排列
个元素的一个排列
1 分类计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有
分类计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有 种不同的方法,在第二类办法中有
种不同的方法,在第二类办法中有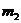 种不同的方法,……,在第n类办法中有
种不同的方法,……,在第n类办法中有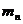 种不同的方法
种不同的方法 那么完成这件事共有
那么完成这件事共有 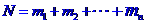 种不同的方法
种不同的方法
2.分步计数原理:做一件事情,完成它需要分成n个步骤,做第一步有 种不同的方法,做第二步有
种不同的方法,做第二步有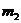 种不同的方法,……,做第n步有
种不同的方法,……,做第n步有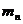 种不同的方法,那么完成这件事有
种不同的方法,那么完成这件事有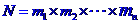 种不同的方法
种不同的方法 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com