
学会了解,理解的重要性,谈成功,面对困难的方法,解决问题的关键,打开成功大门的钥匙……
哪些观点是正确的,哪些观点是错误的?
怎么知道对错呢?我们可以用正确的审题方法来试一试,那正确的审题方法有哪些呢?
1、抓住关键词句法。2、因果推断法。3、明辩关系法。4、对应“人生”法(适合比喻、象征型题目)(具体内容参看《作文备考教程(五)》)
7.如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=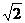 ,PB⊥PD.
,PB⊥PD.
(1)求异面直线PD与BC所成角的余弦值;
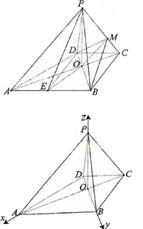 (2)求二面角P-AB-C的大小;
(2)求二面角P-AB-C的大小;
(3)设点M在棱PC上,且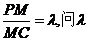 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
解:
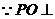 平面
平面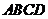
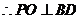 ,又
,又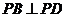 ,
,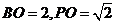 ,
,
由平面几何知识得: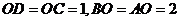
以 为原点,
为原点,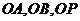 分别为
分别为 轴建立如图所示的空间直角坐标系,则各点坐标为
轴建立如图所示的空间直角坐标系,则各点坐标为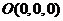 ,
,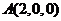 ,
,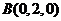 ,
,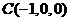 ,
,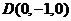 ,
,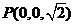
(1)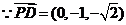 ,
, 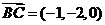 ,
,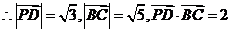 。
。
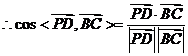
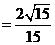 。
。
故直线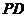 与
与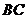 所成的角的余弦值为
所成的角的余弦值为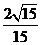
(2)设平面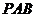 的一个法向量为
的一个法向量为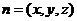 ,
,
由于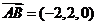 ,
,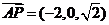 ,
,
由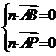 得
得 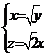 取
取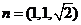 ,
,
又已知平面ABCD的一个法向量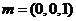 ,
,
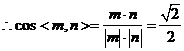 ,
,
又二面角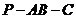 为锐角,
为锐角, 所求二面角
所求二面角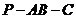 的大小为
的大小为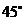
(3)设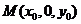 ,由于
,由于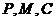 三点共线,
三点共线,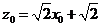 ,
,
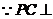 平面
平面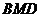 ,
,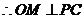
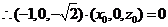
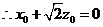
由(1)(2)知: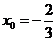 ,
,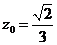 。
。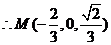
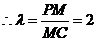 ,故
,故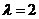 时,
时,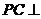 平面
平面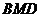 。
。
考查运用空间向量的有关知识求空间的角和距离.要求掌握利用空间向量求空间的角和距离的一般方法.
利用空间向量求异面直线所成角时,必须注意异面直线所成角的范围是(0,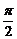
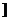 ,向量的夹角的范围是[0,
,向量的夹角的范围是[0,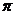
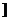 ,故向量的夹角与异面直线的夹角可能相等,也可能互补。
,故向量的夹角与异面直线的夹角可能相等,也可能互补。
求直线与平面所成角:先求出平面的法向量,再求此直线所在向量与法向量所成角(锐角),它的余角为线面角;
求两个平面所成角:二面角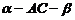 的大小转化为求面
的大小转化为求面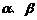 的法向量m、n的夹角<m,n>或其补角。
的法向量m、n的夹角<m,n>或其补角。
空间的距离有:可以利用|a|=a a,进行计算。
a,进行计算。
6.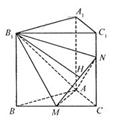 如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱CC1上的点,且CN=2C1N.
如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1,M是底面BC边上的中点,N是侧棱CC1上的点,且CN=2C1N.
(1)求二面角B1-AM-N的平面角的余弦值;
(2)求点B1到平面AMN的距离。
解:(1)建立如图所示的空间直角坐标系,则 (0,0,1),M(0,
(0,0,1),M(0,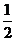 ,0),C(0,1,0), N (0,1,
,0),C(0,1,0), N (0,1,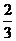 ) , A (
) , A (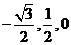 ),
),
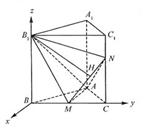 所以,
所以,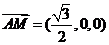 ,
,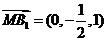 ,
,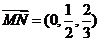 。
。
因为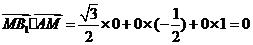
所以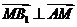 ,同法可得
,同法可得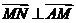 。
。
故﹤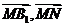 ﹥为二面角
﹥为二面角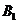 -AM-N的平面角
-AM-N的平面角
∴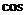 ﹤
﹤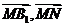 ﹥=
﹥=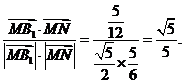
故所求二面角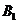 -AM-N的平面角的余弦值为
-AM-N的平面角的余弦值为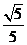 。
。
(2)设n=(x,y,z)为平面AMN的一个法向量,则
由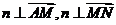 得
得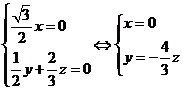 .故可取
.故可取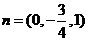
设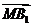 与n的夹角为a,则
与n的夹角为a,则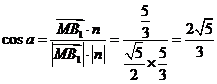 。
。
所以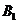 到平面AMN的距离为
到平面AMN的距离为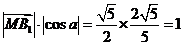 。
。
5.如图,在棱长为1的正方体 中,
中,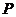 是侧棱
是侧棱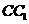 上的一点,
上的一点,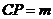 。
。
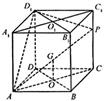 (1)试确定
(1)试确定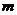 ,使直线
,使直线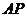 与平面
与平面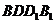 所成角的正切值为
所成角的正切值为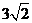 ;
;
(2)在线段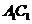 上是否存在一个定点
上是否存在一个定点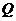 ,使得对任意的
,使得对任意的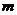 ,
,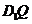 在平面
在平面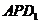 上的射影垂直于
上的射影垂直于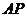 ,并证明你的结论。
,并证明你的结论。
解:(1)建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1).
所以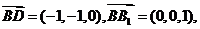
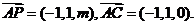
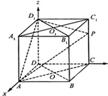 又由
又由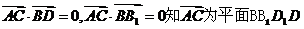 的一个法向量.
的一个法向量.
设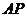 与
与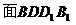 所成的角为
所成的角为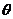 ,
,
则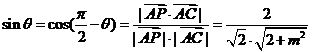
依题意有: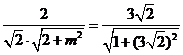 ,解得
,解得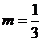 .
.
故当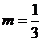 时,直线
时,直线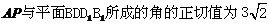 。
。
(2)若在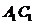 上存在这样的点
上存在这样的点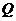 ,设此点的横坐标为
,设此点的横坐标为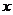 ,
,
则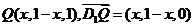 。
。
依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP。
等价于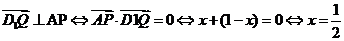
即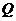 为
为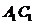 的中点时,满足题设的要求.
的中点时,满足题设的要求.
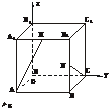
4.如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
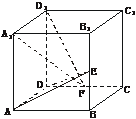
(1)证明AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明面AED⊥面A1D1F.
解:取D为原点,DA、DC、DD1为x轴、y轴、z轴建立直角坐标系,取正方体棱长为2,则A(2,0,0)、A1(2,0,2)、
D1(0,0,2)、E(2,2,1)、F(0,1,0).
(1)∵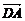 ·
·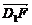 =(2,0,0)·(0,1,-2)=0,∴AD⊥D1F.
=(2,0,0)·(0,1,-2)=0,∴AD⊥D1F.
(2)∵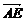 ·
·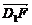 =(0,2,1)·(0,1,-2)=0,∴AE⊥D1F,即AE与D1F成90°角.
=(0,2,1)·(0,1,-2)=0,∴AE⊥D1F,即AE与D1F成90°角.
(3)∵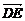 ·
·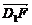 =(2,2,1)·(0,1,-2)=0,∴DE⊥D1F.∵AE⊥D1F,
=(2,2,1)·(0,1,-2)=0,∴DE⊥D1F.∵AE⊥D1F,
∴D1F⊥面AED.∵D1F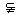 面A1D1F,∴面AED⊥面A1D1F.
面A1D1F,∴面AED⊥面A1D1F.
3.如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求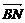 的长;
的长;
(2)求cos〈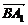 ,
,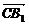 〉的值;
〉的值;
(3)求证:A1B⊥C1M.
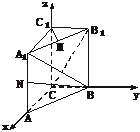
(1)解:依题意得B(0,1,0),N(1,0,1),
∴|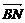 |=
|=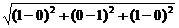 =
=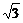 .
.
(2)解:A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),
∴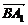 =(1,-1,2),
=(1,-1,2),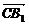 =(0,1,2),
=(0,1,2),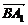 ·
·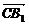 =3,|
=3,|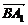 |=
|=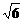 ,|
,|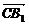 |=
|=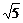 .
.
∴cos〈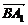 ,
,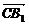 〉=
〉=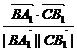 =
=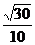 .
.
(3)证明:C1(0,0,2),M(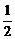 ,
,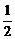 ,2),
,2),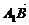 =(-1,1,-2),
=(-1,1,-2),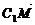 =(
=(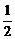 ,
,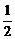 ,0),∴
,0),∴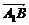 ·
·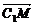 =0,∴A1B⊥C1M.
=0,∴A1B⊥C1M.
2.在正三棱柱ABC-A1B1C1中,各棱长都为a,D是BC中点,则向量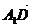 和
和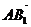 的夹角为_____,异面直线A1D和AB1的夹角为______。
的夹角为_____,异面直线A1D和AB1的夹角为______。
解: cos <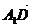 ,
,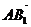 > = -
> = -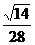 ∴<
∴<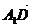 ,
,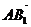 >=π-arccos
>=π-arccos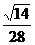
异面直线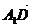 和
和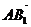 的夹角为φ,则φ= arccos
的夹角为φ,则φ= arccos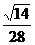
1.在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,那么直线AM与CN所成的角为 ( D )
A.arccos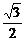 B.arccos
B.arccos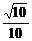
C.arccos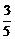 D.arccos
D.arccos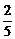
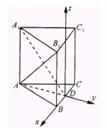 解:建立如图所示坐标系,把D点视作原点O,分别沿
解:建立如图所示坐标系,把D点视作原点O,分别沿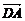 、
、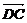 、
、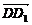 方向为x轴、y轴、z轴的正方向,则α=arccos
方向为x轴、y轴、z轴的正方向,则α=arccos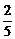 .
.
8.△ABC为边长等于a的正三角形,AE和CD都垂直于平面ABC,且AE=AB=2CD,F是BE的中点。
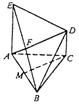 (1)求证:DF//平面ABC;
(1)求证:DF//平面ABC;
(2)求证:AF⊥BD。
证:(1)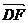 =
=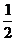 (
(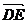 +
+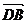 )=
)=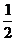 (
(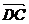 +
+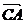 +
+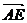 +
+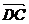 +
+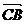 )
)
=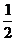 (2
(2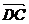 +
+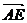 +
+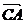 +
+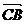 )=
)=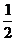 (
(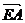 +
+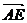 +
+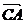 +
+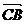 )
)
=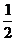 (
(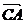 +
+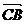 )=
)=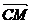 。∴ DF
。∴ DF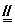 CM,从而DF//平面ABC。
CM,从而DF//平面ABC。
(2)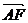 =
=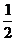 (
(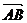 +
+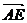 ),
),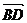 =
=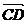 -
-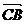 。
。
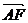 ·
·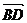 =
=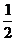 (
(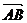 +
+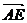 )·(
)·(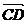 -
-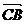 )=
)=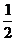 (-
(-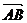 ·
·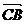 +
+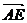 ·
·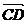 )
)
=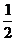 (-
(-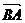 ·
·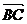 +
+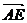 ·
·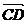 )=
)=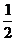 (-|
(-|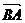 | |
| |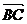 |cos60°+|
|cos60°+|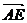 | |
| |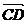 |)
|)
=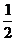 (-
(-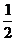 a2+
a2+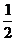 a2)=0。∴ AF⊥BD。
a2)=0。∴ AF⊥BD。
考查运用空间向量的基本知识判断空间的线线、线面位置关系.要求掌握用坐标法或基底法证明空间线面平行、垂直,掌握用空间向量解立体几何问题的一般程序:把已知条件用向量表示,把一些待求的量用基向量或其他向量表示,将几何的位置关系的证明问题或数量关系的运算问题转化为典型的向量运算,以算代证,以值定形.
7.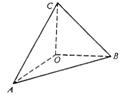 若OA,OB,OC两两互相垂直,求证△ABC为锐角三角形。
若OA,OB,OC两两互相垂直,求证△ABC为锐角三角形。
证明:OA,OB,OC两两互相垂直。
因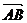 ·
·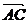 =(
=(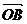 -
-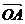 )·(
)·(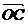 -
-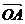 )=
)=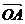 ·
·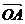 =|
=|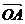 |2>0,
|2>0,
∴ <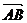 ·
·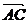 >为锐角,即∠BAC为锐角,
>为锐角,即∠BAC为锐角,
同理∠ABC,∠BCA均为锐角,∴△ABC为锐角三角形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com