
5.周期性
正弦函数、余弦函数都是周期函数,2kπ(k∈Z且k≠0)都是它的周期,最小正周期是2π
4.值域
正弦函数、余弦函数的值域都是[-1,1]
其中正弦函数y=sinx,x∈R
①当且仅当x=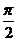 +2kπ,k∈Z时,取得最大值1
+2kπ,k∈Z时,取得最大值1
②当且仅当x=-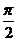 +2kπ,k∈Z时,取得最小值-1
+2kπ,k∈Z时,取得最小值-1
而余弦函数y=cosx,x∈R
①当且仅当x=2kπ,k∈Z时,取得最大值1
②当且仅当x=(2k+1)π,k∈Z时,取得最小值-1
3.定义域:
正弦函数、余弦函数的定义域都是实数集R[或(-∞,+∞)],
分别记作: y=sinx,x∈R y=cosx,x∈R
2.用五点法作正弦函数和余弦函数的简图(描点法):
正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:
(0,0) (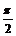 ,1) (p,0) (
,1) (p,0) (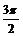 ,-1) (2p,0)
,-1) (2p,0)
余弦函数 y=cosx xÎ[0,2p]的五个点关键是
y=cosx xÎ[0,2p]的五个点关键是
(0,1) (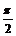 ,0) (p,-1) (
,0) (p,-1) (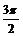 ,0) (2p,1)
,0) (2p,1)
1.y=sinx,x∈R和y=cosx,x∈R的图象,分别叫做正弦曲线和余弦曲线.


21.(13分) 已知函数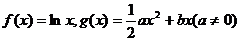 。
。
(1)若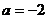 时,函数
时,函数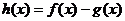 在其定义域内是增函数,求
在其定义域内是增函数,求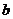 的取值范围;
的取值范围;
(2)在(1)的结论下,设函数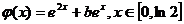 ,求函数
,求函数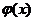 的最小值
的最小值
20. (13分)已知奇函数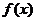 的定义域是
的定义域是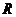 ,且
,且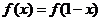 ,当
,当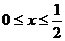 时,
时,
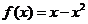 .
.
(1)求证: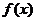 是周期函数;
是周期函数;
(2)求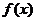 在区间
在区间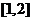 上的解析式;
上的解析式;
(3)求方程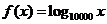 的根的个数.
的根的个数.
19. (13分)在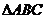 中,
中,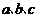 分别为角
分别为角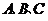 的对边,且满足
的对边,且满足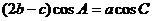
(1)求角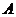 的值;
的值;
(2)若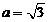 ,设角
,设角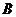 的大小为
的大小为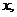
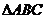 的面积为
的面积为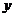 ,求
,求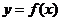 的最大值.m
的最大值.m 
18. (12分) 某企业投入81万元经销某产品,经销时间共60个月,市场调查表明,该企业在经销这个产品期间第 个月的利润
个月的利润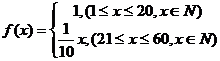 (单位:万元)。为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元)。为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 个月的当月利润率为
个月的当月利润率为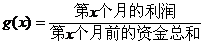 ,例如:
,例如: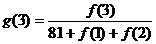 。
。
(1)求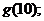
(2)求第 个月的当月利润率
个月的当月利润率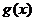 ;
;
(3)该企业经销此产品期间,哪一个月的当前月利润率最大?并求该月的当前利润率。
17. (12分) 已知函数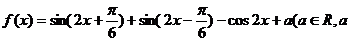 为常数).
为常数).
(1)求函数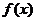 的最小正周期;
的最小正周期;
(2)求函数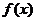 的单调递增区间;
的单调递增区间;
(3) 若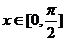 时,
时,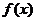 的最小值为
的最小值为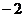 ,求
,求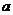 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com