
1.(2009年广东卷文)某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
|
队员i |
1 |
2 |
3 |
4 |
5 |
6 |
|
三分球个数 |
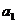 |
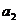 |
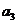 |
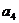 |
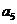 |
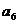 |
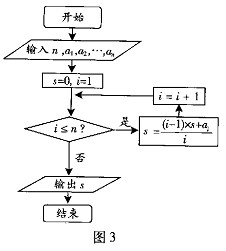
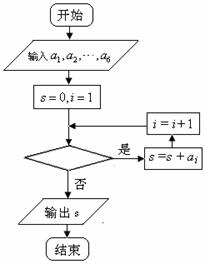
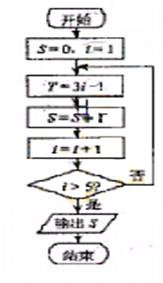
下图(右)是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填 ,输出的s=
(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
21世纪教育网 
 [答案]
[答案]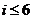 ,
,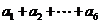
[解析]顺为是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,所图中判断框应填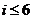 ,输出的s=
,输出的s=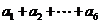 .
.
5.(2009辽宁卷文)某店一个月的收入和支出总共记录了 N个数据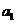 ,
,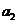 ,。。。
,。。。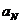 ,其中收入记为正数,支出记为负数。该店用右边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的
,其中收入记为正数,支出记为负数。该店用右边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的
(A)A>0,V=S-T
(B) A<0,V=S-T
(C) A>0, V=S+T
(D)A<0, V=S+T
21世纪教育网 

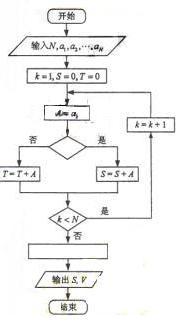
[解析]月总收入为S,因此A>0时归入S,判断框内填A>0
支出T为负数,因此月盈利V=S+T
[答案]C
4.(2009宁夏海南卷理)如果执行上(右)边的程序框图,输入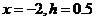 ,那么输出的各个数的合等于
,那么输出的各个数的合等于
(A)3 (B) 3.5 (C) 4 (D)4.5
解析:选B.
3.(2009辽宁卷理)某店一个月的收入和支出总共记录了 N个数据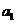 ,
,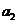 ,。。。
,。。。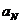 ,其中收入记为正数,支出记为负数。该店用下边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的
,其中收入记为正数,支出记为负数。该店用下边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的
(A)A>0,V=S-T 21世纪教育网 

(B) A<0,V=S-T
(C)
A>0, V=S+T 

(D)A<0, V=S+T

[解析]月总收入为S,因此A>0时归入S,判断框内填A>0
支出T为负数,因此月盈利V=S+T 21世纪教育网 

[答案]C
2.(2009浙江卷文)某程序框图如上(右)图所示,该程序运行后输出的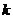 的值是( )
的值是( )
A.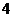 B.
B.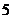
C.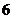 D.
D.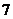
A [命题意图]此题考查了程序语言的概念和基本的应用,通过对程序语言的考查,充分体现了数学程序语言中循环语言的关键.
[解析]对于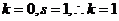 ,而对于
,而对于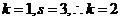 ,则
,则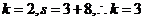 ,后面是
,后面是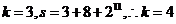 ,不符合条件时输出的
,不符合条件时输出的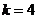 .
.
1.(2009浙江卷理)某程序框图如图所示,该程序运行后输出的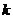 的值是 ( )
的值是 ( )
A.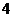 B.
B.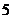 C.
C.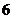 D.
D.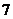
答案:A
 [解析]对于
[解析]对于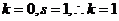 ,而对于
,而对于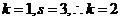 ,则
,则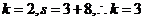 ,后面是
,后面是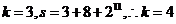 ,不符合条件时输出的
,不符合条件时输出的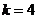 .
.

31.(2009重庆卷文)(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为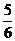 和
和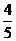 ,且各株大树是否成活互不影响.求移栽的4株大树中:.
,且各株大树是否成活互不影响.求移栽的4株大树中:. 

(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率.
解: 设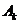 表示第
表示第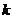 株甲种大树成活,
株甲种大树成活, 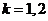 ; 设
; 设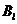 表示第
表示第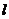 株乙种大树成活,
株乙种大树成活, 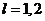
则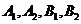 独立,且
独立,且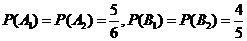
(Ⅰ)至少有1株成活的概率为:
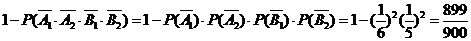
(Ⅱ)由独立重复试验中事件发生的概率公式知,两种大树各成活1株的概率为:
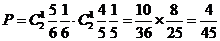 .
. 

30.(2009重庆卷理)(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为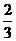 和
和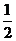 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数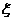 的分布列与期望.
的分布列与期望.


解:设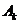 表示甲种大树成活k株,k=0,1,2
表示甲种大树成活k株,k=0,1,2
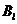 表示乙种大树成活l株,l=0,1,2
表示乙种大树成活l株,l=0,1,2
则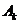 ,
,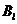 独立. 由独立重复试验中事件发生的概率公式有
独立. 由独立重复试验中事件发生的概率公式有
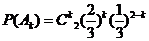 ,
, 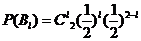 .
.
据此算得
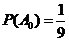 ,
, 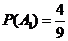 ,
, 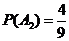 .
.
.
. 

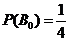 ,
,
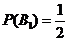 ,
, 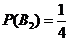 .
.
(Ⅰ) 所求概率为
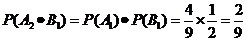 .
.
(Ⅱ) 解法一:
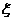 的所有可能值为0,1,2,3,4,且.
的所有可能值为0,1,2,3,4,且. 

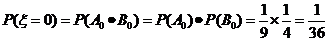 ,
,
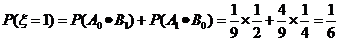 ,
,
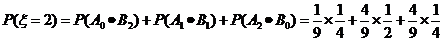
=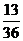 ,
,
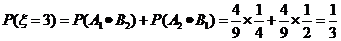 .
.
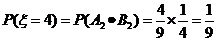 .
.
综上知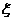 有分布列
有分布列
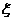 |
0 |
1 |
2 |
3 |
4 |
|
P |
1/36 |
1/6 |
13/36 |
1/3 |
1/9 |
从而,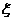 的期望为
的期望为
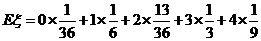
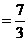 (株)
(株)
解法二:
分布列的求法同上
令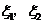 分别表示甲乙两种树成活的株数,则
分别表示甲乙两种树成活的株数,则

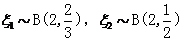
故有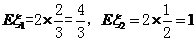 .
. 

从而知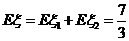
29.(2009福建卷文)(本小题满分12分)
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果;


(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
解:(I)一共有8种不同的结果,列举如下:
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑)
(Ⅱ)记“3次摸球所得总分为5”为事件A
事件A包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件A包含的基本事件数为3
由(I)可知,基本事件总数为8,所以事件A的概率为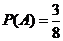 .
. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com