
 家用电器一件
家用电器一件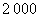 元,实行分期付款,每期为一个月,购买后一个月付款一次,再过一个月又付款一次,共付
元,实行分期付款,每期为一个月,购买后一个月付款一次,再过一个月又付款一次,共付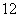 次即购买一年后付清,按月利率
次即购买一年后付清,按月利率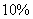 ,每月复利一次计算,则每期应付款
元.
,每月复利一次计算,则每期应付款
元.
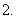 (
(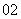 全国)某城市
全国)某城市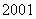 年末汽车保有量为
年末汽车保有量为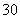 万辆,预计此后每年报废上一年末汽车保有量的
万辆,预计此后每年报废上一年末汽车保有量的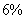 ,并且每年新增汽车数量相同
,并且每年新增汽车数量相同 为了保护城市环境,要求该城市汽车保有量不超过
为了保护城市环境,要求该城市汽车保有量不超过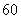 万辆,那么每年新增汽车数量不应超过多少辆?
万辆,那么每年新增汽车数量不应超过多少辆?
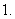 某工厂总产值月增长率为
某工厂总产值月增长率为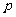 ,则年平均增长率为
,则年平均增长率为
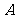
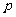
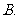
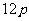
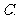
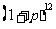
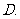
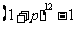
 (
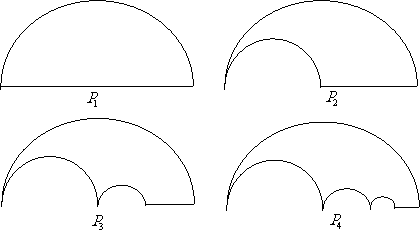
(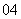 重庆理)如图
重庆理)如图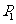 是一块半径为
是一块半径为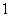 的半圆形纸板,在
的半圆形纸板,在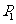 的左下端剪去一个半径为
的左下端剪去一个半径为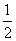 的半圆后得到图形
的半圆后得到图形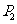 ,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形
,然后依次剪去一个更小半圆(其直径为前一个被剪掉半圆的半径)得圆形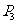 、
、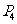 、…,
、…,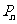 ,…记纸板
,…记纸板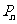 的面积为
的面积为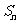 ,则
,则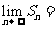
问题1.(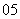 上海)假设某市
上海)假设某市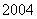 年新建住房
年新建住房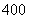 万平方米,其中有
万平方米,其中有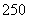 万平方米是中低价房.预计在今后的若干年后,该市每年新建住房面积平均比上年增长
万平方米是中低价房.预计在今后的若干年后,该市每年新建住房面积平均比上年增长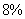 .另外,每年新建住房中,中底价房的面积均比上一年增加
.另外,每年新建住房中,中底价房的面积均比上一年增加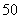 万平方米.那么,到哪一年底
万平方米.那么,到哪一年底
 该市历年所建中低价房的累计面积(以
该市历年所建中低价房的累计面积(以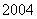 年为累计的第一年)将首次不少于
年为累计的第一年)将首次不少于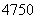 万平方米?
万平方米? 当年建造的中低价房的面积占该年建造住房面积的比例首次大于
当年建造的中低价房的面积占该年建造住房面积的比例首次大于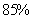 ?
?
问题2.银行按规定每经过一定的时间结算存(贷)款的利息一次,结算后即将利息并入本金,这种计算利息的方法叫做复利.现在有某企业进行技术改造,有两种方案:
甲方案:一次性贷款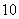 万元,第一年便可获得利润
万元,第一年便可获得利润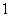 万元,以后每年比上年增加
万元,以后每年比上年增加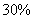 的利润;
的利润;
乙方案:每年贷款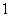 万元,第一年可获得利润
万元,第一年可获得利润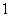 万元,以后每年比前一年多获利
万元,以后每年比前一年多获利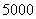 元.
元.
两种方案的期限都是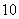 年,到期一次行归还本息.若银行贷款利息均以年息
年,到期一次行归还本息.若银行贷款利息均以年息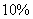 的复利计算,试比较两个方案哪个获得存利润更多?(计算精确到千元,参考数据:
的复利计算,试比较两个方案哪个获得存利润更多?(计算精确到千元,参考数据: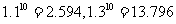 )
)
 问题3.(
问题3.(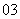 京春)如图,在边长为
京春)如图,在边长为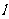 的
的
等边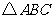 中,
中,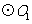 为
为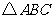 的内切圆,
的内切圆,
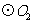 与
与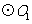 外切,且与
外切,且与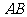 ,
,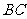 相切,…,
相切,…,
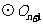 与
与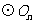 外切,且与
外切,且与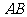 、
、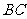 相切,
相切,
如此无限继续下去.记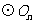 的面积为
的面积为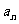
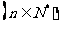 .
.
(Ⅰ)证明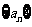 是等比数列;
是等比数列;
(Ⅱ)求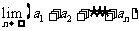 的值.
的值.
问题4.(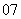 上海) 近年来,太阳能技术运用的步伐日益加快.
上海) 近年来,太阳能技术运用的步伐日益加快.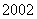 年全球太阳电池的年生产量达到
年全球太阳电池的年生产量达到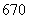 兆瓦,年生产量的增长率为
兆瓦,年生产量的增长率为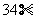 ,以后四年中,年生产量的增长率逐年递增
,以后四年中,年生产量的增长率逐年递增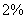 (如
(如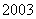 年的年生产量的增长率为
年的年生产量的增长率为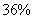 ).
).
 求
求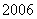 年全球太阳电池的年生产量(结果精确到
年全球太阳电池的年生产量(结果精确到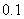 兆瓦);
兆瓦);
 目前太阳电池产业存在的主要问题是市场安装量远小于生产量,
目前太阳电池产业存在的主要问题是市场安装量远小于生产量,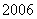 年的实际安装量为
年的实际安装量为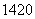 兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持在
兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持在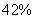 ,到
,到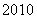 年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的
年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的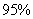 ),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精确到
),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精确到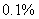 )?
)?
 解答数列应用题要注意步骤的规范性:设数列,判断数列,解题完毕要作答;
解答数列应用题要注意步骤的规范性:设数列,判断数列,解题完毕要作答;
 在归纳或求通项公式时,一定要将项数
在归纳或求通项公式时,一定要将项数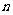 计算准确;
计算准确;
 在数列类型不易分辨时,要注意归纳递推关系;
在数列类型不易分辨时,要注意归纳递推关系;
 在近似计算时,要注意应用对数方法和二项式定理,且要看清题中对近似程度的要求.
在近似计算时,要注意应用对数方法和二项式定理,且要看清题中对近似程度的要求.
 解应用问题的核心是建立数学模型;
解应用问题的核心是建立数学模型;
 一般步骤:审题、抓住数量关系、建立数学模型;
一般步骤:审题、抓住数量关系、建立数学模型;
 注意问题是求什么(
注意问题是求什么(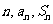 ).
).
 (
(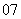 陕西)已知各项全不为零的数列
陕西)已知各项全不为零的数列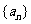 的前
的前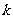 项和为
项和为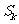 ,且
,且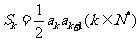 ,其中
,其中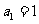 .
.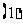 求数列
求数列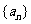 的通项公式;
的通项公式; 对任意给定的正整数
对任意给定的正整数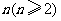 ,数列
,数列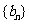 满足
满足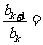
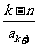 (
(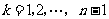 ),
),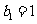 ,求
,求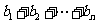 .
.
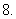 (
(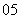 湖北文)设数列
湖北文)设数列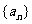 的前
的前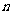 项和为
项和为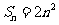 ,
,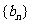 为等比数列,且
为等比数列,且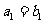 ,
,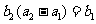 ,
,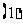 求数列
求数列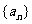 和
和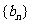 的通项公式;
的通项公式;
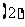 设
设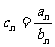 ,求数列
,求数列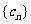 的前
的前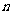 项和
项和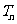
 (
(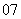 陕西文)已知实数列
陕西文)已知实数列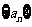 是等比数列,其中
是等比数列,其中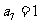 ,且
,且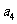 ,
,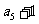 ,
,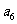 成等差数列.(Ⅰ)求数列
成等差数列.(Ⅰ)求数列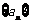 的通项公式;
的通项公式;
(Ⅱ)数列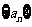 的前
的前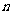 项和记为
项和记为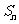 ,证明:
,证明:
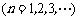 .
.
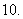 (
(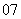 湖南文)设
湖南文)设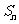 是数列
是数列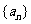 (
(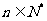 )的前
)的前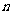 项和,
项和,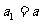 ,且
,且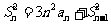 ,
,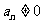 ,
,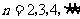 .
.
(Ⅰ)证明:数列 (
(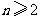 )是常数数列;
)是常数数列;
(Ⅱ)试找出一个奇数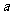 ,使以
,使以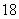 为首项,
为首项,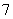 为公比的等比数列
为公比的等比数列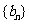 (
(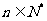 )中的所有项都是数列
)中的所有项都是数列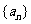 中的项,并指出
中的项,并指出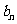 是数列
是数列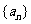 中的第几项.
中的第几项.
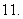 (
(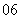 北京)在数列
北京)在数列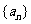 中,若
中,若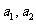 是正整数,且
是正整数,且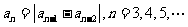 ,
,
则称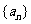 为“绝对差数列”.
为“绝对差数列”.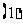 举出一个前五项不为零的“绝对差数列”(只要求写出前十项);
举出一个前五项不为零的“绝对差数列”(只要求写出前十项); 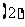 若“绝对差数列”
若“绝对差数列”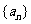 中,
中,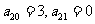 ,数列
,数列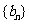 满足
满足 ,
,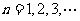 ,分别判断当
,分别判断当 时,
时,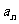 与
与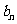 的极限是否存在,如果存在,求出其极限值;
的极限是否存在,如果存在,求出其极限值;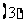 证明:任何“绝对差数列”中总含有无穷多个为零的项.
证明:任何“绝对差数列”中总含有无穷多个为零的项.
 (
(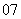 上海)如果有穷数列
上海)如果有穷数列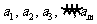 (
(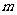 为正整数)满足条件
为正整数)满足条件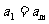 ,
,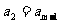 ,…,
,…,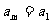 ,即
,即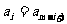 (
(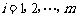 ),我们称其为“对称数列”.
),我们称其为“对称数列”.
例如,数列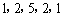 与数列
与数列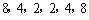 都是“对称数列”.
都是“对称数列”.
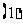 设
设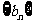 是
是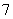 项的“对称数列”,其中
项的“对称数列”,其中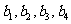 是等差数列,且
是等差数列,且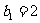 ,
,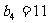 .依次写出
.依次写出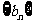 的每一项;
的每一项;
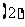 设
设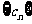 是
是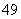 项的“对称数列”,其中
项的“对称数列”,其中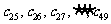 是首项为
是首项为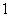 ,公比为
,公比为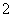 的等比数列,求
的等比数列,求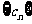 各项的和
各项的和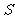 ;
;
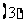 设
设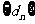 是
是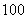 项的“对称数列”,其中
项的“对称数列”,其中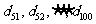 是首项为
是首项为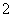 ,公差为
,公差为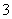 的等差数列.求
的等差数列.求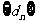 前
前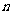 项的和
项的和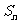
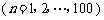 .
.
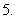 (
(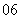 浙江文)若
浙江文)若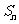 是公差不为
是公差不为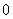 的等差数列
的等差数列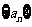 的前
的前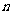 项和,且
项和,且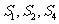 成等比数列.
成等比数列.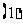 求数列
求数列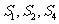 的公比;
的公比;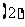 若
若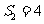 ,求
,求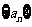 的通项公式.
的通项公式.
 (
(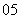 福建)已知
福建)已知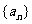 是公比为
是公比为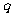 的等比数列,且
的等比数列,且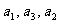 成等差数列.
成等差数列.
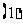 求
求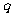 的值;
的值;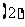 设{
设{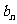 }是以
}是以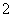 为首项,
为首项,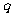 为公差的等差数列,其前
为公差的等差数列,其前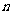 项和为
项和为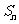 ,当
,当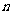 ≥
≥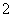 时,比较
时,比较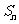 与
与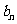 的大小,并说明理由.
的大小,并说明理由.
 (
( 上海)在等差数列
上海)在等差数列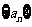 中,若
中,若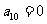 ,则有不等式
,则有不等式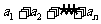
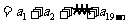
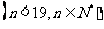 成立,相应地:在等比数列
成立,相应地:在等比数列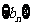 ,若
,若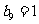 ,
则有不等式
成立.
,
则有不等式
成立.
 (
(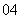 北京)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和. 已知数列
北京)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和. 已知数列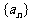 是等和数列,且
是等和数列,且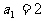 ,公和为
,公和为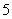 ,那么
,那么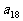 的值为_____,这个数列的前
的值为_____,这个数列的前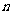 项和
项和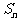 的计算公式为________
的计算公式为________
 (
(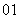 新课程)设
新课程)设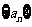 是公比为
是公比为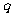 的等比数列,
的等比数列,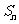 是它的前
是它的前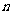 项和,若
项和,若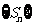 是等差数列,则
是等差数列,则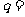
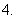 有四个数,其中前三个数成等差数列,后三个数成等比数列,且第一个数与第四个数的和是
有四个数,其中前三个数成等差数列,后三个数成等比数列,且第一个数与第四个数的和是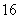 ,第二个数与第三个数的和是
,第二个数与第三个数的和是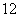 ,求这四个数.
,求这四个数.
问题1.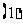 (
( 湖北)若互不相等的实数
湖北)若互不相等的实数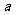 、
、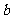 、
、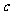 成等差数列,
成等差数列,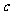 、
、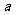 、
、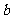 成等比数列,且
成等比数列,且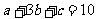 ,则
,则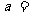
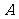
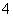
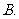
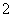
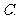

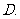

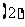 (
( 天津)设等差数列
天津)设等差数列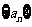 的公差
的公差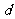 不为
不为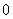 ,
,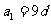 .若
.若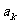 是
是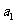 与
与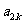 的等比中项,则
的等比中项,则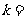
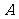
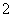
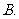
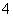
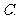
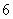
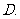
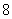
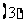 (
(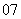 海南)已知
海南)已知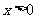 ,
,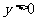 ,
,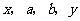 成等差数列,
成等差数列,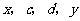 成等比数列,则
成等比数列,则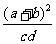 的最小值是
的最小值是 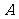
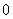
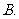
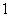
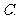
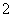
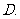
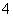
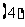 已知等差数列
已知等差数列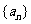 的公差
的公差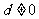 ,且
,且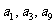 成等比数列,则
成等比数列,则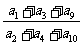
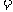
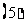 (
(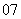 全国Ⅰ)等比数列
全国Ⅰ)等比数列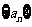 的前
的前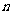 项和为
项和为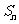 ,已知
,已知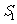 ,
,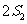 ,
,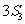 成等差数列,
成等差数列,
则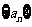 的公比为
的公比为
问题2.(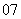 全国Ⅰ文)设
全国Ⅰ文)设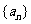 是等差数列,
是等差数列,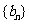 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且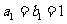 ,
,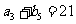 ,
,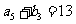
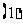 求
求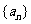 ,
,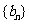 的通项公式;
的通项公式;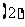 求数列
求数列 的前
的前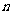 项和
项和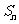 .
.
问题3.(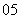 全国Ⅲ)在等差数列
全国Ⅲ)在等差数列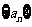 中,公差
中,公差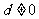 ,
,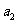 是
是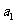 与
与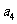 的等比中项,已知数列
的等比中项,已知数列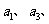
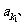
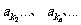 成等比数列,求数列
成等比数列,求数列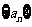 的通项
的通项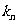
问题4.(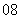 届东北师大附中高三月考)数列
届东北师大附中高三月考)数列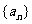 的前
的前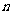 项和记作
项和记作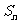 ,满足
,满足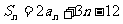 ,
,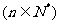 .
.
 证明数列
证明数列 为等比数列;并求出数列
为等比数列;并求出数列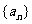 的通项公式.
的通项公式.
 记
记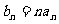 ,数列
,数列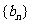 的前
的前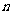 项和为
项和为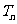 ,求
,求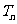 .
.
问题5.( 上海) 已知数列
上海) 已知数列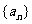 (
(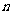 为正整数)是首项是
为正整数)是首项是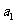 ,公比为
,公比为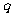 的等比数列.
的等比数列.
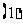 求和:
求和: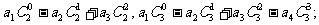
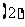 由
由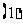 的结果归纳概括出关于正整数
的结果归纳概括出关于正整数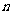 的一个结论,并加以证明.
的一个结论,并加以证明.
 解决等差数列和等比数列的问题时,通常考虑两类方法:①基本量法:即运用条件转化为关于
解决等差数列和等比数列的问题时,通常考虑两类方法:①基本量法:即运用条件转化为关于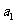 和
和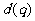 的方程;②巧妙运用等差数列和等比数列的性质,一般地运用性质可以化繁为简,减少运算量.
的方程;②巧妙运用等差数列和等比数列的性质,一般地运用性质可以化繁为简,减少运算量.
 深刻领会两类数列的性质,弄清通项和前
深刻领会两类数列的性质,弄清通项和前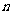 项和公式的内在联系是解题的关键.
项和公式的内在联系是解题的关键.
 解题时,还要注重数学思想方法的应用,如“函数与方程”、“数形结合”、“分类讨论”、
解题时,还要注重数学思想方法的应用,如“函数与方程”、“数形结合”、“分类讨论”、
“化归转化”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com