
 会用坐标变换法,求一条曲线
会用坐标变换法,求一条曲线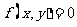 按向量
按向量 平移后所得的曲线方程
平移后所得的曲线方程
 会把函数图像的平移问题转化为按向量平移的问题 .
会把函数图像的平移问题转化为按向量平移的问题 .
 数学思想方法:化归思想、方程思想、待定系数法.
数学思想方法:化归思想、方程思想、待定系数法.

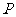 点位置与点
点位置与点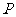 分
分 所成的比
所成的比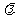 的关系:
的关系:
 设
设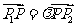 ,且
,且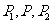 的坐标分别为
的坐标分别为 ,则有
,则有
 将点
将点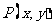 按向量
按向量 平移后所得的点为
平移后所得的点为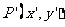 ,则
,则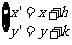
 把函数
把函数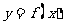 的图像按
的图像按 平移,就相当于把函数的图像左右平移
平移,就相当于把函数的图像左右平移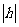 个单位,再上下平移
个单位,再上下平移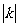 个单位.
个单位.
 (
( 湖北文)设
湖北文)设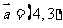 ,
,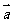 在
在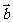 上的投影为
上的投影为 ,
,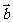 在
在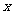 轴上的投影为
轴上的投影为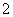 ,且
,且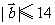 ,则
,则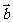 为
为 
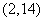
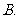
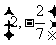

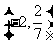

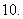 (
( 全国Ⅰ)已知向量
全国Ⅰ)已知向量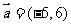 ,
,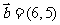 ,则
,则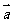 与
与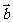
 垂直
垂直
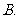 不垂直也不平行
不垂直也不平行  平行且同向
平行且同向 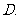 平行且反向
平行且反向
 (
( 北京文)已知向量
北京文)已知向量 ,
,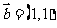 .若向量
.若向量 ,则实数
,则实数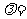
 (
( 重庆文)已知向量
重庆文)已知向量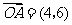 ,
,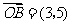 ,且
,且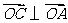 ,
, ,则
,则
向量

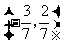
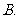
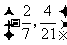

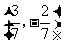
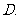
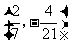
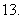 (
(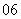 山东)设向量
山东)设向量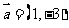 ,
,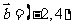 ,
, ,若表示向量
,若表示向量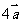 ,
, ,
,
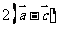 ,
,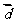 的有向线段首尾相接能构成四边形,则向量
的有向线段首尾相接能构成四边形,则向量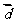 为
为

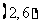
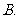


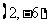
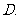
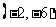
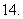 (
(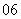 重庆)与向量
重庆)与向量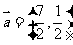 ,
, 的夹角相等,且模为
的夹角相等,且模为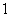 的向量是
的向量是

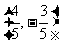
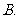
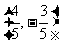 或
或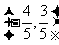


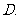
 或
或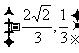
 (
(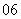 辽宁)设
辽宁)设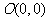 ,
, ,
,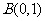 ,点
,点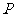 是线段
是线段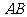 上的一个动点,
上的一个动点,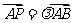 ,若
,若 ,则实数
,则实数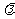 的取值范围是
的取值范围是

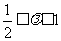
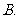
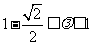

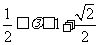
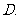

 (
(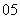 全国Ⅱ)已知点
全国Ⅱ)已知点 ,
,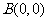 ,
,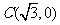 .设
.设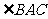 的平分线
的平分线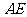 与
与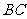
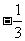
相交于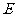 ,那么有
,那么有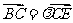 ,其中
,其中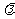 等于
等于 
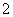
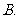
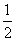


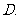
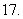 (
(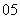 天津)在直角坐标系
天津)在直角坐标系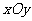 中,已知点
中,已知点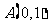 和点
和点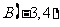 ,若点
,若点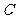 在
在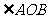 的平分线上且
的平分线上且 ,则
,则
 (
( 湖北文)设过点
湖北文)设过点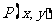 的直线分别与
的直线分别与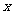 轴的正半轴和
轴的正半轴和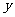 轴的正半轴交于
轴的正半轴交于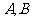
两点,点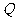 与点
与点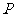 关于
关于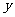 轴对称,
轴对称,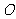 为坐标原点,若
为坐标原点,若 且
且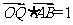 ,
,
则点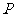 的轨迹方程是
的轨迹方程是


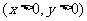
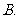
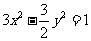
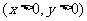

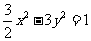
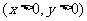
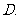

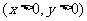
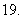 (
(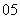 全国Ⅲ)已知向量
全国Ⅲ)已知向量 ,
,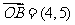 ,
, ,且
,且 三点共线,则
三点共线,则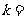
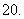 (
(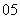 山东)已知向量
山东)已知向量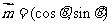 和
和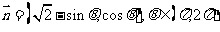 ,且
,且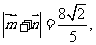 求
求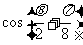 的值.
的值.
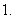 三点
三点 共线的充要条件是
共线的充要条件是

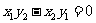
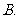
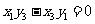

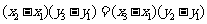
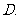

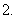 如果
如果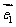 ,
,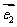 是平面
是平面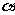 内所有向量的一组基底,那么下列命题中正确的是
内所有向量的一组基底,那么下列命题中正确的是
 若实数
若实数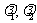 使
使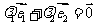 ,则
,则 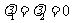
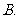 空间任一向量
空间任一向量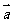 可以表示为
可以表示为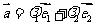 ,这里
,这里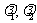 是实数
是实数
 对实数
对实数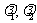 ,向量
,向量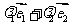 不一定在平面
不一定在平面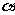 内
内
 对平面内任一向量
对平面内任一向量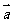 ,使
,使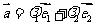 的实数
的实数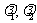 有无数对
有无数对
 已知向量
已知向量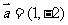 ,
,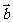 与
与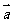 方向相反,且
方向相反,且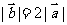 ,那么向量
,那么向量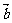 的坐标是_
的坐标是_
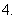 已知
已知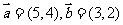 ,则与
,则与 平行的单位向量的坐标为
平行的单位向量的坐标为
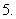 已知
已知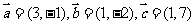 ,求
,求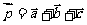 ,并以
,并以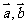 为基底来表示
为基底来表示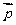
 设
设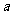 、
、 为正数,且
为正数,且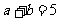 ,则
,则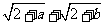 的最大值为
的最大值为
 已知向量
已知向量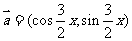 ,
, 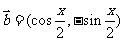 ;
;
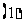 当
当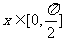 ,求
,求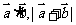 ;
;
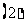 若
若 ≥
≥ 对一切实数
对一切实数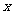 都成立,求实数
都成立,求实数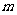 的范围
的范围
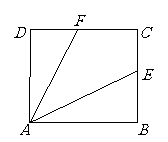
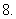 设
设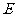 、
、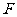 分别是正方形
分别是正方形 中
中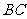 、
、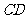
两边的中点,求 的值
的值
问题1.(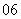 全国Ⅱ)已知向量
全国Ⅱ)已知向量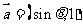 ,
,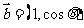 ,
,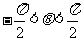
(Ⅰ)若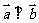 ,求
,求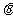 ;(Ⅱ)求
;(Ⅱ)求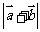 的最大值.
的最大值.
问题2.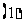 已知
已知 ,
,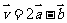 ,且
,且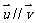 ,求实数
,求实数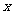
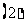 已知向量
已知向量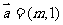 ,
,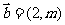 的夹角为钝角,求
的夹角为钝角,求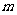 的取值范围.
的取值范围.
 (
(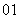 新课程)若向量
新课程)若向量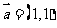 ,
,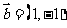 ,
,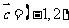 ,则
,则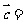

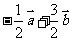
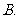
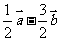


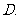

问题3.已知点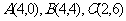 ,试用向量方法求直线
,试用向量方法求直线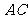 和
和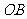 (
(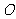 为坐标原点)交点
为坐标原点)交点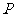 的坐标.
的坐标.
问题4.设椭圆方程为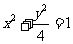 ,过
,过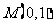 的直线
的直线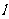 交椭圆于
交椭圆于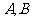 两点,
两点,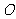 为坐标原点,动点
为坐标原点,动点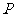 满足
满足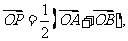 ,点
,点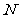 的坐标为
的坐标为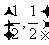 ,当
,当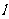 绕点
绕点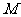 旋转时.
旋转时.
 求动点
求动点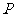 的轨迹方程;
的轨迹方程;
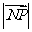 的最大值与最小值
的最大值与最小值
 建立坐标系解决问题(数形结合);
建立坐标系解决问题(数形结合); 认清向量的方向求坐标;
认清向量的方向求坐标;
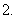 ①若
①若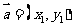 ,
,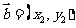 ,则
,则 ;
;
②若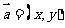 ,则
,则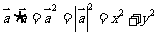 ,
,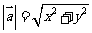 ;
;
③若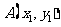 ,
,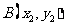 ,则
,则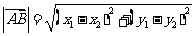 ;
;
④若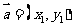 ,
,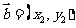 ,则
,则 ;
;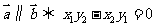
 重要不等式:
重要不等式: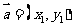 ,
,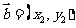 ,则
,则 ≤
≤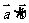 ≤
≤
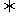
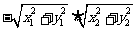 ≤
≤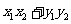 ≤
≤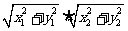
 (
(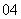 上海春)在
上海春)在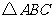 中,有命题:①
中,有命题:① ;②
;②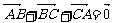 ;
;
③若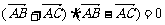 ,则
,则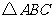 为等腰三角形;④若
为等腰三角形;④若 ,
,
则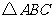 为锐角三角形.上述命题正确的是
为锐角三角形.上述命题正确的是
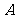 ①②
①②
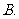 ①④
①④ 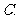 ②③
②③
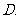 ②③④
②③④
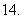 (
( 陕西)已知非零向量
陕西)已知非零向量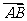 与
与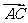 满足
满足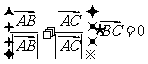 且
且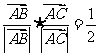 , 则
, 则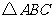 为
为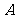 等边三角形
等边三角形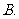 直角三角形
直角三角形 等腰非等边三角形
等腰非等边三角形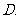 三边均不相等的三角形
三边均不相等的三角形
 (
( 上海文)若向量
上海文)若向量 的夹角为
的夹角为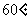 ,
,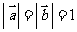 ,则
,则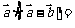
 (
( 浙江)若非零向量
浙江)若非零向量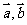 满足
满足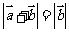 ,则
,则
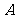

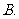

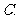
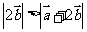
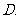

 (
( 全国Ⅰ文)点
全国Ⅰ文)点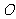 是
是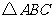 所在平面内的一点,满足
所在平面内的一点,满足
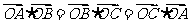 ,则点
,则点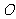 是
是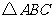 的
的
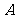 三个内角的角平分线的交点
三个内角的角平分线的交点 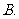 三条边的垂直平分线的交点
三条边的垂直平分线的交点
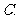 三条中线的交点
三条中线的交点 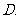 三条高的交点
三条高的交点
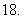
 (
( 天津)如图,在
天津)如图,在 中,
中,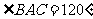 ,
,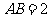 ,
,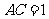 ,
,
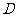 是边
是边 上一点,
上一点,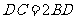 ,则
,则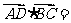

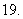 (
( 重庆)如图,在四边形
重庆)如图,在四边形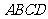 中,
中, ,
,
 ,
,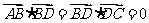 ,
,
则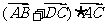 的值为
的值为 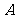
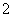
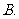
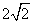
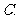
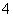
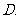
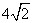
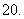 (
( 辽宁)若向量
辽宁)若向量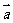 与
与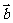 不共线,
不共线, ,且
,且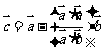 ,则向量
,则向量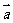 与
与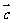 的夹角为
的夹角为 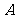
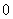
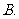

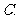
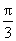
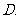
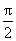
 (
( 湖南)设
湖南)设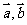 是非零向量,若函数
是非零向量,若函数 的图象是一条直线,
的图象是一条直线,
则必有 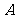
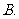
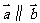
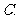

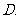

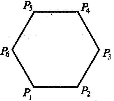 (
( 四川)如图, 已知正六边形
四川)如图, 已知正六边形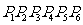 ,下列向量的数量积中最大的是
,下列向量的数量积中最大的是
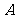
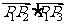
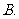
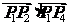
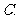
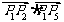
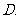

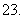 (
( 湖北文)已知非零向量
湖北文)已知非零向量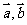 ,若
,若 与
与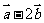 互相垂直,则
互相垂直,则
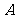

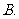
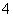
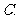
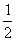
 (
(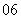 浙江)设向量
浙江)设向量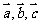 满足
满足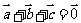 ,
,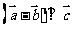 ,
,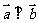 ,若
,若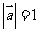 ,
,
则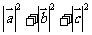 的值是
的值是
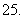 (
(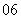 全国Ⅰ文)已知向量
全国Ⅰ文)已知向量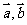 满足
满足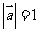 ,
,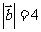 ,且
,且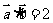 ,则
,则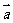 与
与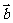 的夹角为
的夹角为
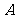
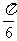
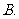
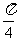
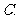
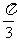
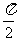
 (
(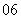 北京)若
北京)若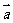 与
与  都是非零向量,则“
都是非零向量,则“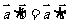 ”是“
”是“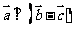 ”的
”的
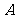 充分不必要条件
充分不必要条件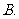 必要不充分条件
必要不充分条件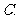 充分必要条件
充分必要条件 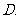 既不充分也不必要条件
既不充分也不必要条件
 (
(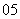 北京)若
北京)若 ,且
,且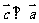 ,则向量
,则向量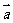 与
与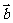 的夹角为
的夹角为
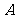
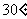
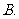
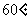
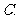
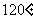
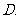
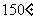
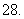 (
( 天津文)已知
天津文)已知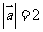 ,
,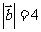 ,
,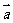 与
与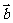 的夹角为
的夹角为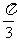 ,以
,以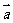 ,
,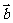 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
 (
(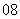 届高三江西师大附中期中试题)若两个向量
届高三江西师大附中期中试题)若两个向量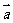 与
与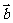 的夹角为
的夹角为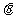 ,则称向量“
,则称向量“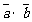 ”为“向量积”,其长度
”为“向量积”,其长度 . 若
. 若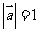 ,
, ,
,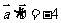 ,求
,求
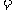
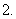 已知
已知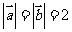 ,
,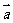 与
与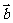 的夹角为
的夹角为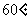 ,则
,则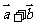 在
在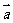 上的投影为
上的投影为
 向量
向量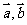 都是非零向量,且
都是非零向量,且 ,求
,求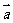 与
与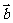 的夹角
的夹角
 已知两单位向量
已知两单位向量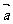 与
与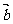 的夹角为
的夹角为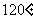 ,若
,若 ,
,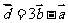 ,试求
,试求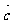 与
与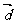 的夹角。
的夹角。
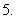 已知向量
已知向量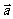 和
和 的夹角是
的夹角是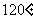 ,且
,且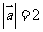 ,
, ,则
,则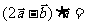
 设向量
设向量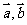 满足
满足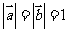 ,
,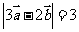 ,则
,则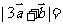
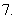 已知向量
已知向量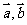 的方向相同,且
的方向相同,且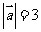 ,
, ,则
,则
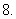 在
在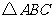 中,
中, ,
,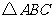 的面积是
的面积是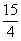 ,若
,若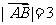 ,
, ,则
,则
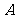

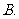
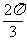
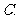

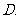
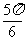
 已知
已知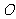 为原点,点
为原点,点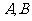 的坐标分别为
的坐标分别为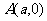 ,
,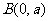 ,其中常数
,其中常数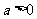 ,点
,点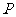 在线段
在线段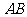 上,且有
上,且有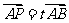
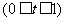 ,则
,则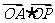 的最大值为
的最大值为 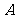

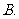
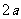
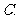
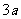
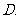
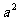
 设
设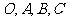 为平面上四个点,
为平面上四个点,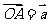 ,
,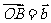 ,
,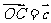 ,且
,且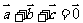 ,
, 
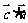
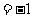 ,则
,则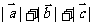 =
=
 设两个向量
设两个向量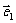 、
、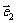 ,满足
,满足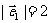 ,
,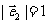 ,
,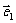 、
、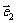 的夹角为
的夹角为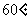 ,若向量
,若向量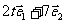 与向量
与向量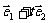 的夹角为钝角,求实数
的夹角为钝角,求实数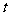 的取值范围.
的取值范围.
 (
( 届高三湖北八校联考)在
届高三湖北八校联考)在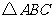 中,
中,
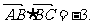
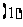 求
求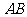 边的长度;
边的长度;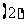 求
求 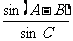 的值
的值
问题1.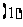 有下列命题:①
有下列命题:①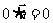 ;②
;② 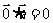 ;③若
;③若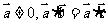 ,
,
则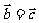 ;④若
;④若 ,则
,则 当且仅当
当且仅当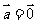 时成立;⑤
时成立;⑤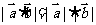
⑥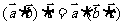 对任意
对任意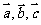 向量都成立;⑦对任意向量
向量都成立;⑦对任意向量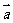 ,有
,有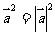

其中正确命题的序号是
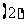 (
( 福建)对于向量
福建)对于向量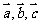 和实数
和实数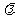 ,下列命题中真命题是
,下列命题中真命题是
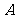 若
若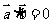 ,则
,则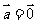 或
或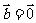
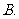 若
若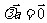 ,则
,则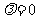 或
或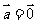
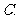 若
若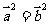 ,则
,则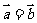 或
或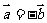
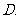 若
若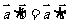 ,则
,则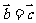
问题2. 已知
已知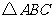 中,
中,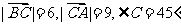 ,则
,则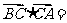
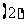 (
( 浙江)已知平面上三点
浙江)已知平面上三点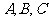 满足
满足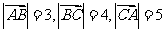 ,
,
则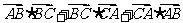 的值等于
的值等于
 已知
已知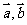 是两个非零向量,且
是两个非零向量,且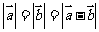 ,求
,求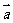 与
与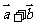 的夹角
的夹角
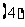 (
(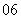 福建文)已知向量
福建文)已知向量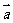 与
与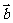 的夹角为
的夹角为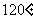 ,
,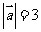 ,
,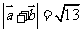 ,则
,则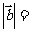
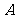
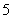
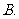
问题3.(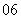 苏锡常镇模拟)已知平面上三个向量
苏锡常镇模拟)已知平面上三个向量 ,它们之间的夹角均为
,它们之间的夹角均为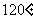 .
.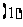 求证:
求证: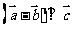 ;
;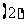 若
若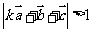
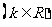 ,求
,求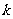 的取值范围.
的取值范围.
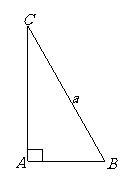
问题4. (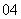 湖北)如图,在
湖北)如图,在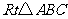 中,已知
中,已知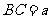 ,若
,若
长为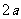 的线段
的线段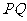 以点
以点 为中点,问
为中点,问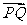 与
与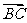 的夹角
的夹角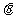 取何值时
取何值时
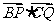 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com