7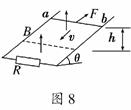．如图8所示的电路中，两根光滑金属导轨平行放置在倾角为θ的斜面上，导轨下端接有电阻R，导轨电阻不计，斜面处在竖直向上的磁感应强度为B的匀强磁场中，电阻可略去不计的金属棒ab质量为m，受到沿斜面向上且与金属棒垂直的恒力F的作用，金属棒沿导轨匀速下滑，则它在下滑h高度的过程中，以下说法正确的是　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．作用在金属棒上各力的合力做功为零

B．重力做功将机械能转化为电能

C．重力与恒力F做功的代数和等于电阻R上产生的焦耳热

D．金属棒克服安培力做功等于重力与恒力F做的总功与电阻R上产生的焦耳热之和

解析：由于金属棒匀速下滑，故作用在棒上的各个力的合力做功为零，故A对；克服安培力做功将机械能转化为电能，故B错误；列出动能定理方程W_G－W_F－W_安＝0，变形可得W_G－W_F＝W_安，可知C正确，D错误．

答案：AC

6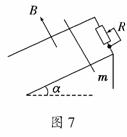．(2010··徐州模拟模拟)如图7所示，有两根和水平方向成α角的光滑平行的金属轨道，上端接有可变电阻R，下端足够长，空间有垂直于轨道平面的匀强磁场，磁感应强度为B.一根质量为m的金属杆从轨道上由静止滑下，经过足够长的时间后，金属杆的速度会趋近于一个最大速度v_m，则　　　　　　　　　　　　　　　　　　　　 (　)

A．如果B增大，v_m将变大

B．如果α变大，v_m将变大

C．如果R变大，v_m将变大

D．如果m变小，v_m将变大

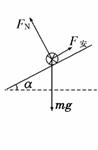
解析：以金属杆为研究对象，受力如图所示．

根据牛顿第二定律得

mgsinα－F_安＝ma，其中F_安＝.

当a→0时，v→v_m，

解得v_m＝，

结合此式分析即得B、C选项正确．

答案：BC

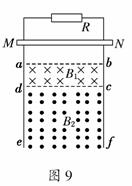
5．(2010·扬州模拟)如图5甲所示，光滑导轨水平放置在与水平方向夹角为60°的斜向下的匀强磁场中，匀强磁场的磁感应强度B随时间t的变化规律如图5乙所示(规定斜向下为正方向)，导体棒ab垂直导轨放置，除电阻R的阻值外，其余电阻不计，导体棒ab在水平外力F作用下始终处于静止状态．规定a→b的方向为电流的正方向，水平向右的方向为外力F的正方向，则在0-t₁时间内，图6中能正确反映流过导体棒ab的电流i和导体棒ab所受水平外力F随时间t变化的图象是　　　　　　　　　　　　 　(　)

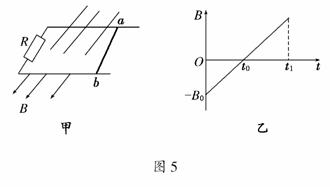
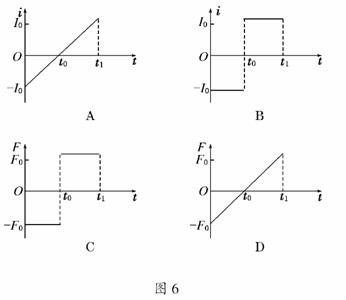
解析：由楞次定律可判定回路中的电流方向始终为b→a，由法拉第电磁感应定律可判定回路中电流大小恒定，故A、B错；由F_安＝BIL可得F_安随B的变化而变化，在0-t₀时间内，F_安方向向右，故外力F与F_安等值反向，方向向左为负值；在t₀-t₁时间内，F_安方向改变，故外力F方向也改变为正值，故C错误，D正确．

答案：D

4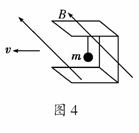．如图4所示，有一用铝板制成的U型框，将一质量为m的带电小球用绝缘细线悬挂在框中，使整体在匀强磁场中沿垂直于磁场方向向左以速度v匀速运动，悬挂拉力为F_T，则(　)

A．悬线竖直，F_T＝mg

B．悬线竖直，F_T>mg

C．悬线竖直，F_T<mg

D．无法确定F_T的大小和方向

解析：设两板间的距离为L，由于向左运动的过程中竖直板切割磁感线，产生动生电动势，由右手定则判断下板电势高于上板，动生电动势大小E＝BLv，即带电小球处于电势差为BLv的电场中，所受电场力F_电＝qE_电＝q＝q＝qvB.

设小球带正电，则所受电场力方向向上．

同时小球所受洛伦兹力F_洛＝qvB，方向由左手定则判断竖直向下，即F_电＝F_洛，所以F_T＝mg.同理分析可知当小球带负电时，F_T＝mg.故无论小球带什么电，F_T＝mg.选项A正确．

答案：A

3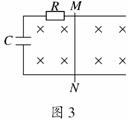．如图3所示，两光滑平行金属导轨间距为L，直导线MN垂直跨在导轨上，且与导轨接触良好，整个装置处于垂直纸面向里的匀强磁场中，磁感应强度为B.电容器的电容为C，除电阻R外，导轨和导线的电阻均不计．现给导线MN一初速度，使导线MN向右运动，当电路稳定后，MN以速度v向右做匀速运动，则　　　　　　　　　　　　　　　　　　　

(　)

A．电容器两端的电压为零

B．电阻两端的电压为BLv

C．电容器所带电荷量为CBLv

D．为保持MN匀速运动，需对其施加的拉力大小为

解析：当导线MN匀速向右运动时，导线MN产生的感应电动势恒定，稳定后，电容器既不充电也不放电，无电流产生，故电阻两端无电压，电容器两极板间电压U＝E＝BLv，所带电荷量Q＝CU＝CBLv，故A、B错，C对；MN匀速运动时，因无电流而不受安培力，故拉力为零，D错．

答案：C

2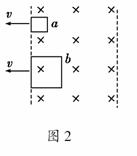．如图2所示，用粗细相同的铜丝做成边长分别为L和2L的两只闭合线框a和b，以相同的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外，不考虑线框的动能，若外力对环做的功分别为W_a、W_b，则W_a∶W_b为　　　　　　　 (　)

A．1∶4　 　　　　　　B．1∶2

C．1∶1 　　　　　　D．不能确定

解析：根据能量守恒可知，外力做的功等于产生的电能，而产生的电能又全部转化为焦耳热

W_a＝Q_a＝·　W_b＝Q_b＝·

由电阻定律知R_b＝2R_a，故W_a∶W_b＝1∶4.A项正确．

答案：A

1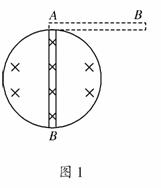．如图1所示，竖直平面内有一金属环，半径为a，总电阻为　　

R(指拉直时两端的电阻)，磁感应强度为B的匀强磁场垂直

穿过环平面，在环的最高点A用铰链连接长度为2a、电阻

为的导体棒AB，AB由水平位置紧贴环面摆下，当摆到竖

直位置时，B点的线速度为v，则这时AB两端的电压大小

为　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　B. 　　　　　　C. 　　　D．Bav

解析：摆到竖直位置时，AB切割磁感线的瞬时感应电动势E＝B·2a·(v)＝Bav.由闭合电路欧姆定律，

U_AB＝·＝Bav，故选A.

答案：A

12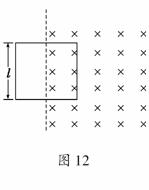．(14分)(2009·全国卷Ⅱ)如图12所示，匀强磁场的磁感应强度方向垂直于纸面向里，大小随时间的变化率＝k，k为负的常量．用电阻率为ρ、横截面积为S的硬导线做成一边长为l的方框，将方框固定于纸面内，其右半部位于磁场区域中．求：

(1)导线中感应电流的大小；

(2)磁场对方框作用力的大小随时间的变化率．

解析：(1)导线框的感应电动势为

E＝　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　①

ΔΦ＝l²ΔB　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

导线框中的电流为

I＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

式中R是导线框的电阻，根据电阻率公式有

R＝ρ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

联立①②③④式，将＝k代入得

I＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

(2)导线框所受磁场的作用力的大小为

F＝BIl　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　⑥

它随时间的变化率为

＝Il　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑦

由⑤⑦式得

＝.

答案：(1)　(2)

11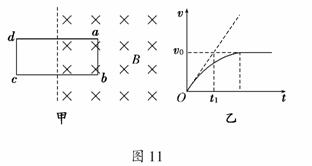．(12分)如图11甲所示，竖直向下的匀强磁场垂直于光滑的桌面，图甲中的虚线为磁场的边界线，边界线右侧的磁场区域足够大；质量为m、电阻为R的矩形金属线圈abcd平放在桌面上，线圈的长和宽分别为l和2l，线圈的一半在磁场内，一半在磁场外；t＝0时刻磁感应强度从B₀开始均匀减小，线圈中产生感应电流，在磁场力作用下线圈的v－t图象如图11乙所示，图乙中的斜向虚线为t＝0时刻速度图线的切线，数据由图中给出．求：

(1)t＝0时刻金属线圈的加速度；

(2)磁感应强度的变化率.

解析：(1)由v－t图象知，t＝0时刻的加速度为

a＝＝.

　(2)t＝0时刻

E＝·S＝·l²

回路中电流I＝

此时安培力F＝B₀Il

由牛顿第二定律得F＝ma

联立上述各式得＝.

答案：(1)　(2)

10．(11分)(2010·常州模拟)如图10甲所示，一正方形金属线框位于有界匀强磁场区域内，线框的右边紧贴着边界．t＝0时刻对线框施加一水平向右的外力F，让线框从静止开始做匀加速直线运动，经过时间t₀穿出磁场．图10乙所示为外力F随时间t变化的图象．若线框质量为m、电阻R及图象中的F₀、t₀均为已知量，则根据上述条件，请你推出：

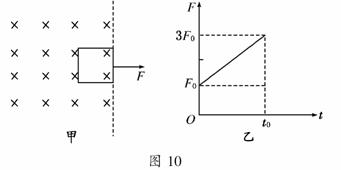
　(1)磁感应强度B的表达式；

(2)线框左边刚离开磁场前瞬间的感应电动势E的表达式．

解析：(1)线框运动的加速度：a＝　　　　　　　　　　　　　　　　　　　 ①

线框边长：l＝at₀²②

线框离开磁场前瞬间速度：

v＝at₀ ③

由牛顿第二定律知：

3F₀－＝ma　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　④

解①②③④式得，

B＝ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

(2)线框离开磁场前瞬间感应电动势：

E＝Blv　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

解①②③⑤⑥式得：E＝ .

答案：(1) 　(2)