231.如图2－35：在空间四边形ABCD中，已知BC＝AC，AD＝BD，引BE⊥CD，E为垂足，作AH⊥BE于H，求证：AH⊥平面BCD。

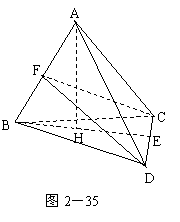解析： 要证AH⊥平面BCD，只须利用直线和平面垂直的判定定理，证AH垂直于平面BCD中两条相交直线即可。

证明:取AB中点F，连结CF、DF， ∵AC＝BC，∴CF⊥AB， 又∵AD＝BD，∴DF⊥AB，∴AB⊥平面CDF， 又CD平面CDF，∴CD⊥AB 又CD⊥BE，∴CD⊥平面ABE，CD⊥AH 又AH⊥BE，∴AH⊥平面BCD。

点评:证明线面垂直，需转化为线线垂直，而线线垂直，又可通过证线面垂直来实现。在这里，定义可以双向使用，即直线a垂直于平面α内的任何直线，则a⊥α，反之，若a⊥α，则a垂直于平面α内的任何直线。

5．三条共点直线两两垂直，设为a，b，c且a，b，c共点于O， ∵a⊥b，a⊥c，b∩c＝0，且c确定一平面，设为α，则a⊥α， 同理可知b垂直于由a，c确定的平面，c垂直于由a，b确定的平面 ∴该命题应打“√”

点评:此类问题必须做到：概念清楚、问题理解透彻、相关知道能灵活运用。

4．前面介绍了两个命题，①过一点有且只有一个平面与已知直线垂直，②过一点有且只有一条直线与已知平面垂直，根据第一个命题知：过点A垂直于直线a的平面惟一，因此，过点A且与直线a垂直的直线都在过点A且与直线a垂直的平面内，∴该命题应打“√”

3．垂直于三角形两边的直线必垂直于三角形所在的平面，由线面垂直定义的逆用，则该直线必垂直于三角形的第三边，∴该命题应打“√”

2．该命题的关键是这无数条直线具有怎样的位置关系，若为平行，则该命题应打“√”号；若为相交，则该命题应打“×”号，正是因为这两种可能同时具备，因此，不说明面内这无数条线的位置关系，则该命题应打“×”号

5．如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面 (　)

解析： 本题是利用直线和平面垂直的定义及判定定理等知识来解答的问题。

解答: 1．直线与平面平行，则直线与平面内的直线的位置关系不外乎有两种①平行，②异面，因此应打×

4．过点A垂直于直线a的所有直线都在过点A垂直于a的平面内　　　　　　　 (　)

3．垂直于三角形两边的直线必垂直于第三边　　　　　　　　　　　　　　　　 (　)

2．如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直　　　　 (　)

1．一条直线和一个平面平行，它就和这个平面内的任何直线平行　　　　　　　 (　)