
11.2008淅江宁波)2008年5月1日,目前世界上最长的跨海大桥--杭州湾跨海大桥通车了.通车后,苏南A地到宁波港的路程比原来缩短了120千米.已知运输车速度不变时,行驶时间将从原来的3时20分缩短到2时.
(1)求A地经杭州湾跨海大桥到宁波港的路程.
(2)若货物运输费用包括运输成本和时间成本,已知某车货物从A地到宁波港的运输成本是每千米1.8元,时间成本是每时28元,那么该车货物从A地经杭州湾跨海大桥到宁波港的运输费用是多少元?
(3)A地准备开辟宁波方向的外运路线,即货物从A地经杭州湾跨海大桥到宁波港,再从宁波港运到B地.若有一批货物(不超过10车)从A地按外运路线运到B地的运费需8320元,其中从A地经杭州湾跨海大桥到宁波港的每车运输费用与(2)中相同,从宁波港到B地的海上运费对一批不超过10车的货物计费方式是:一车800元,当货物每增加1车时,每车的海上运费就减少20元,问这批货物有几车?
10.(2008山东烟台)如图,抛物线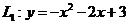 交
交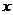 轴于A、B两点,交
轴于A、B两点,交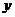 轴于M点.抛物线
轴于M点.抛物线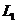 向右平移2个单位后得到抛物线
向右平移2个单位后得到抛物线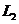 ,
,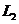 交
交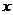 轴于C、D两点.
轴于C、D两点.
(1)求抛物线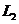 对应的函数表达式;
对应的函数表达式;
(2)抛物线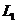 或
或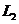 在
在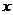 轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
轴上方的部分是否存在点N,使以A,C,M,N为顶点的四边形是平行四边形.若存在,求出点N的坐标;若不存在,请说明理由;
(3)若点P是抛物线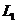 上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线
上的一个动点(P不与点A、B重合),那么点P关于原点的对称点Q是否在抛物线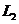 上,请说明理由.
上,请说明理由.
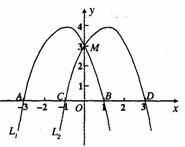
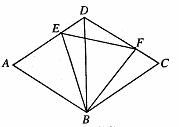
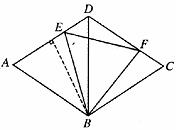
9.(2008山东烟台)如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由;
(3)设△BEF的面积为S,求S的取值范围.
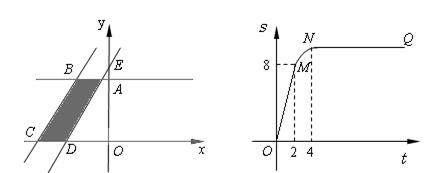
8. (2008浙江义乌)如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与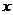 轴负半轴上.过点B、C作直线
轴负半轴上.过点B、C作直线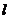 .将直线
.将直线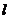 平移,平移后的直线
平移,平移后的直线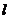 与
与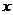 轴交于点D,与
轴交于点D,与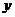 轴交于点E.
轴交于点E.
(1)将直线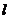 向右平移,设平移距离CD为
向右平移,设平移距离CD为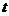 (t
(t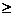 0),直角梯形OABC被直线
0),直角梯形OABC被直线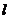 扫过的面积(图中阴影部份)为
扫过的面积(图中阴影部份)为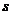 ,
,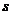 关于
关于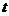 的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当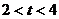 时,求S关于
时,求S关于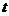 的函数解析式;
的函数解析式;
(2)在第(1)题的条件下,当直线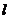 向左或向右平移时(包括
向左或向右平移时(包括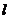 与直线BC重合),在直线AB上是否存在点P,使
与直线BC重合),在直线AB上是否存在点P,使 为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
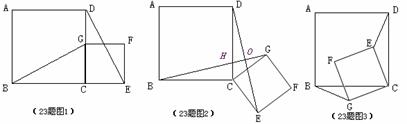
7.(2008浙江义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度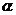 ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
 (2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka, CG=kb (a
(2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka, CG=kb (a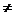 b,k
b,k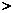 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结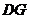 、
、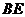 ,且a=3,b=2,k=
,且a=3,b=2,k=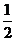 ,求
,求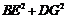 的值.
的值.
6. (2008浙江金华)如图1,在平面直角坐标系中,己知ΔAOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD.(1)求直线AB的解析式;(2)当点P运动到点( ,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于
,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于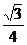 ,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
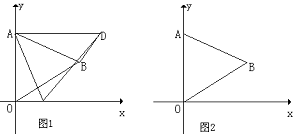
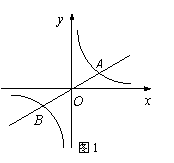
5、(2007浙江金华)如图1,已知双曲线y= (k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;
(k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;
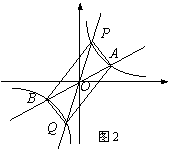
(2)如图2,过原点O作另一条直线l,交双曲线y= (k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行四边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出mn应满足的条件;若不可能,请说明理由.
(k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行四边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出mn应满足的条件;若不可能,请说明理由.


4.(08山东省日照市)在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?



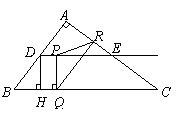
3. (08浙江温州)如图,在 中,
中,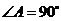 ,
,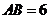 ,
,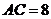 ,
, 分别是边
分别是边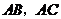 的中点,点
的中点,点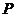 从点
从点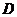 出发沿
出发沿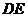 方向运动,过点
方向运动,过点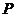 作
作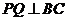 于
于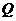 ,过点
,过点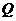 作
作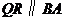 交
交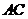 于
于
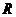 ,当点
,当点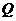 与点
与点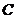 重合时,点
重合时,点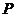 停止运动.设
停止运动.设 ,
,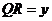 .
.
(1)求点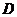 到
到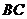 的距离
的距离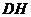 的长;
的长;
(2)求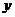 关于
关于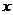 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点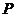 ,使
,使 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的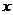 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
2. (08浙江衢州)已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,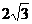 ),C(0,
),C(0,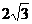 ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;
(2)当纸片重叠部分的图形是四边形时,求t的取值范围;
(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com