
5、sinA = cos(90°- ); cosA = sin( - );tanA =cot( ); cotA = 。
4、tan A•cotA = ; tan B•cotB = ;
3、正弦、余弦值的大小范围: <sin A< ; <cos A<
2、锐角三角函数值,都是 实数(正、负或者0);
1、锐角∠A的三角函数(按右图Rt△ABC填空)
∠A的正弦:sinA = ,∠A的余弦:cosA = ,∠A的正切:tanA = , ∠A的余切:cotA =
29、

27. _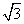 _______. 28___
_______. 28___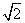 _______
_______
25.(1)证明:∵在△ABC与△EFD中,AB=EF,由EF∥AB得∠BAC=∠FED.由AD= CE得AC=ED.
∴△ABC≌△EFD.
(2)四边形BDFC是平行四边形.
证明:∵△ABC≌△EFD,
∴BC=FD,∠BCA=∠EDF.
∴BC∥FD
∴四边形BDFC是平行四边形.
26剖析:解题时,注意区分判定定理与性质定理的不同使用.
∵□ 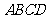 中,
中,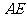 ∥
∥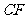 ,∴
,∴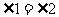 .
.
 又
又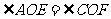 ,
,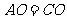 .
.
∴△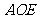 ≌△
≌△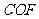 ,∴
,∴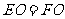 .
.
∴四边形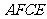 是平行四边形 .
是平行四边形 .
又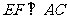 ,∴□
,∴□ 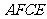 是菱形.
是菱形.
24.:可连结DH,证明 ΔDHE≌ΔDHF或连结EF,通过证明等腰三角形得证。
证: ⑴∵AD∥BC ∴AD∥CE 又∵DE∥AC ∴四边形ACED是平行四边形
⑵过D点作DF⊥BE于F点 ∵DE∥AC,AC⊥BD ∴DE⊥BD,即∠BDE=90°
由⑴知DE=AC,CE=AD=3 ∵四边形ABCD是等腰梯形 ∴AC=DB
∴DE=DB ∴△DBE是等腰直角三角形,∴△DFB也是等腰直角三角形
∴DF=BF=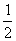 (7-3)+3=5 (也可运用:直角三角形斜边上的中线等于斜边的一半“)
(7-3)+3=5 (也可运用:直角三角形斜边上的中线等于斜边的一半“)
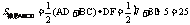 注:⑴过对角线交点O作OF⊥BC于F,延长FO交AD于H,于是OH⊥AD由△ABC≌△DCB,得到△OBC是等腰直角三角形,OF=
注:⑴过对角线交点O作OF⊥BC于F,延长FO交AD于H,于是OH⊥AD由△ABC≌△DCB,得到△OBC是等腰直角三角形,OF=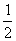 BC=
BC=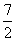 同理OH=
同理OH=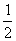 AD=
AD=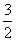 ,高HF=
,高HF=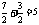 ⑵过A作AF⊥BC于F,过D作DH⊥BC于H,由△AFC≌△DHB
得高AF=FC=
⑵过A作AF⊥BC于F,过D作DH⊥BC于H,由△AFC≌△DHB
得高AF=FC=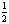 (AD+BC)=5⑶
(AD+BC)=5⑶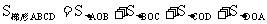 (进行计算)
(进行计算)
解:(1)当CE=4时,四边形ABED是等腰梯形。 理由如下:
在BC上截取CE=AD,连结DE、AE,∵AD∥BC, ∴四边形AECD是平行四边形。
∴AE=CD=BD。 ∵BE=12-4=8>4,即BE>AD, ∴AB不平行于DE,
∴四边形ABED是梯形。 ∵AE∥CD,CD=BD, ∴∠AEB=∠C=∠DBC。
在△ABE和△DEB中,
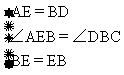 ∴△ABE≌△DEB (SAS)。 ∴AB=DE,
∴△ABE≌△DEB (SAS)。 ∴AB=DE,
∴四边形ABED是等腰梯形。 (也可不作辅助线,通过证明△ABD≌EDC而得AB=DE)
(2)当C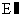 =6时,四边形AB
=6时,四边形AB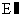 D是直角梯形。 理由如下: 在BC上取一点
D是直角梯形。 理由如下: 在BC上取一点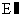 ,使C
,使C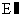 =B
=B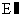 =
=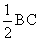 =6,连结D
=6,连结D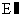 , ∵BD=CD ∴D
, ∵BD=CD ∴D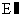 ⊥BC 又∵B
⊥BC 又∵B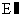 ≠AD,AD∥B
≠AD,AD∥B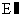 , ∴AB不平行于D
, ∴AB不平行于D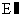 ∴四边形AB
∴四边形AB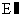 D是直角梯形。
D是直角梯形。
23、∵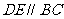 ,
,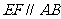
∴四边形DBFE是平行四边形
∴ DE=BF,
∵ 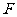 是
是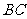 的中点.
的中点.
∴BF=CF
∴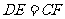
证明:∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形 ∴DE=BF
∵F是BC的中点 ∴BF=CF ∴DE=CF
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com