
7.函数、方程、不等式之间的转化
例11.(2009山东省济宁市)若函数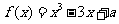 有三个不同的零点,则实数
有三个不同的零点,则实数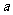 的取值范围是
的取值范围是
A.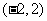 B.
B.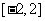 C.
C. D.
D.
分析:本题为三次函数有三个不同的零点,则函数应该有两个极值点,一个极值为正,一个极值为负,所以要先求出其导数,再求其极值。
解: 由函数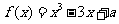 有三个不同的零点,则函数
有三个不同的零点,则函数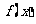 有两个极值点,且有
有两个极值点,且有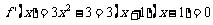 ,得
,得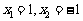 ,所以函数
,所以函数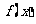 的两个极值为
的两个极值为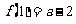 和
和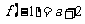 ,结合图象,应该有
,结合图象,应该有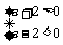 ∴
∴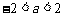 ,故选A
,故选A
答案:A
评注:一般地对于高次函数来说,要转化为导函数研究问题,特别是在研究函数的单调性、最值等性质时要用导数解决。
例12.设函数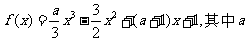 为实数。
为实数。
(Ⅰ)已知函数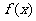 在
在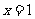 处取得极值,求
处取得极值,求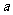 的值;
的值;
(Ⅱ)已知不等式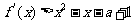 对任意
对任意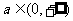 都成立,求实数
都成立,求实数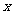 的取值范围。
的取值范围。
分析:(Ⅱ)中不等式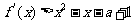 对任意
对任意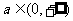 都成立,可以转化为
都成立,可以转化为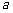 的不等式在
的不等式在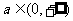 都成立,从而变为
都成立,从而变为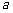 的一次函数由单调性来解答;也可以将
的一次函数由单调性来解答;也可以将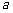 分化出来,转化为
分化出来,转化为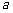 的不等式在
的不等式在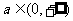 恒成立,研究右边函数的最值。
恒成立,研究右边函数的最值。
解: (1)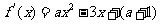 ,由于函数
,由于函数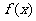 在
在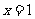 时取得极值,所以
时取得极值,所以 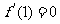
即 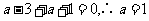
(2) 方法一: 由题设知: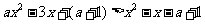 对任意
对任意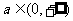 都成立
都成立
即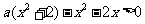 对任意
对任意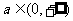 都成立
都成立
设 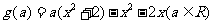 , 则对任意
, 则对任意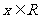 ,
,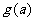 为单调递增函数
为单调递增函数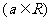
所以对任意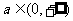 ,
,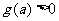 恒成立的充分必要条件是
恒成立的充分必要条件是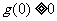
即 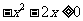 ,
,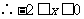 , 于是
, 于是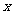 的取值范围是
的取值范围是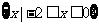
方法二:由题设知: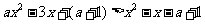 对任意
对任意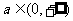 都成立
都成立
即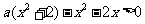 对任意
对任意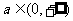 都成立
都成立
于是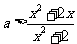 对任意
对任意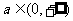 都成立,即
都成立,即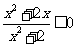
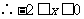 , 于是
, 于是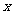 的取值范围是
的取值范围是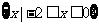
评注:对于不等式恒成立问题,一般来说是要分化出参数,转化为求右边函数的最值问题;但有的也不容易分化,我们也可以转换主变量,把二次函数转化为一次函数,根据一次函数的单调性即可容易完成。
(湖北理)
已知定义在正实数集上的函数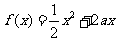 ,
,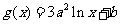 ,其中
,其中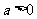 .设两曲线
.设两曲线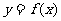 ,
,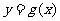 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用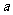 表示
表示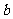 ,并求
,并求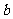 的最大值;
的最大值;
(II)求证: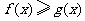 (
(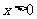 ).
).
本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力.
解:(Ⅰ)设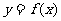 与
与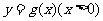 在公共点
在公共点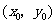 处的切线相同.
处的切线相同.
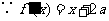 ,
,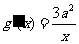 ,由题意
,由题意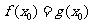 ,
,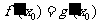 .
.
即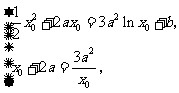 由
由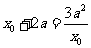 得:
得: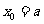 ,或
,或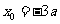 (舍去).
(舍去).
即有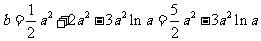 .
.
令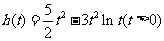 ,则
,则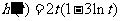 .于是
.于是
当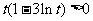 ,即
,即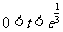 时,
时,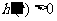 ;
;
当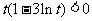 ,即
,即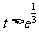 时,
时,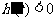 .
.
故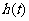 在
在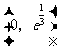 为增函数,在
为增函数,在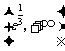 为减函数,
为减函数,
于是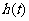 在
在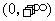 的最大值为
的最大值为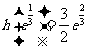 .
.
(Ⅱ)设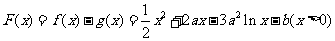 ,
,
则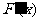
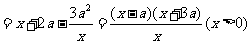 .
.
故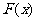 在
在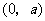 为减函数,在
为减函数,在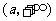 为增函数,
为增函数,
于是函数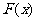 在
在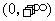 上的最小值是
上的最小值是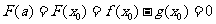 .
.
故当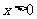 时,有
时,有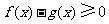 ,即当
,即当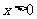 时,
时,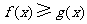 .
.
6.极坐标与参数方程转化为普通方程
例10.(2008南通四县)(坐标系与参数方程)已知曲线C的极坐标方程是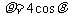 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: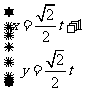 ,求直线l与曲线C相交所成的弦的弦长.
,求直线l与曲线C相交所成的弦的弦长.
分析:本题既有参数方程又有极坐标方程,用极坐标方程和参数方程研究弦长问题很难解决,可以转化为普通方程求出。
解:曲线C的极坐标方程是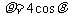 化为直角坐标方程为
化为直角坐标方程为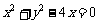 ,即
,即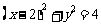 直线l的参数方程
直线l的参数方程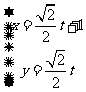 ,化为普通方程为x-y-1=0,
,化为普通方程为x-y-1=0,
曲线C的圆心(2,0)到直线l的距离为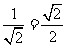
所以直线l与曲线C相交所成的弦的弦长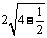 =
=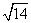 .
.
评注:研究极坐标与参数方程问题可以直接研究,也可以转化为普通方程研究,特别是在研究直线与圆锥曲线的位置关系时常常转化为普通方程求出。
5.三视图转化为立体图
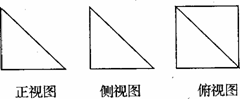 例8.(2009莱阳模拟)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n这样的几何体拼成一个棱长为4的正方体,则V,n的值是(
)
例8.(2009莱阳模拟)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为4的两个全等的等腰直角三角形.若该几何体的体积为V,并且可以用n这样的几何体拼成一个棱长为4的正方体,则V,n的值是(
)
A.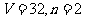 B.
B.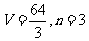
C.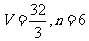 D.
D.
分析:由三视图转化为立体图,再做解答。
解:根据三视图,可知此几何体为一个如图所示的四棱锥,其体积为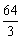 ,故选B
,故选B
答案:B
评注:高考题注重对立体几何中的三视图的考查,一般是给出几何体的三视图,让我们还原为立体图,然后求出一些几何量。
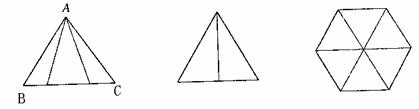
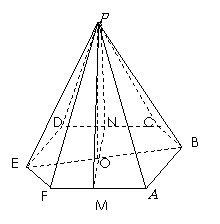
例9.(2008山东淄博市模拟)一个几何体的三视图如下图所示,其中正视图中△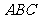 是边长为
是边长为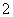 的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为(
)
的正三角形,俯视图为正六边形,那么该几何体的侧视图的面积为(
)
 正视图
侧视图
俯视图
正视图
侧视图
俯视图
A. 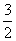 B.
B.
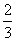 C.
C.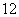 D.
D.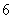
分析:先把三视图还原为立体图,再由立体图进行解答。
解:有三视图可知,此几何体为正六棱锥,如图,其中正视图
为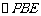 ,是正三角形,则
,是正三角形,则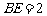 ,∴底面边长为1,侧棱长为2,
,∴底面边长为1,侧棱长为2,
则高为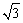 ,设
,设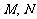 分别为
分别为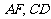 的中点,则
的中点,则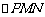 为侧视图,
为侧视图,
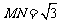 ,∴侧视图的面积为
,∴侧视图的面积为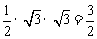 ,故选
,故选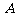 。
。
答案: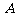
评注:正确对待三视图,要会还原为立体图,找出相应的量解出,
注意对应的量不能出错。
4.函数与导函数之间的转化
例6.(2008湖北卷,理7)若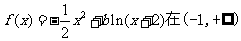 上是减函数,则
上是减函数,则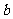 的取值范围是
(
)
的取值范围是
(
)
A. 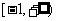 B.
B. 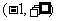 C.
C.  D.
D. 
分析:把已知条件函数在某区间上是单调减函数需要转化为函数的导函数在此区间上是恒负,再分化出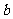 ,转化为函数研究最值问题解决。
,转化为函数研究最值问题解决。
解:∵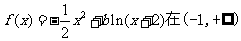 上是减函数,∴
上是减函数,∴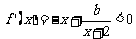 在
在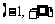 上恒成立,即
上恒成立,即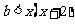 在
在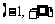 上恒成立,设
上恒成立,设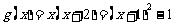 在
在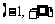 上单调递增,∴
上单调递增,∴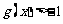 ,∴当
,∴当 时,
时,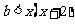 在
在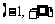 上恒成立,即
上恒成立,即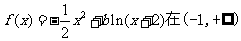 上是减函数。故选C
上是减函数。故选C
答案:C
评注:函数的单调性通常转化为导函数的正负判断,而不等式恒成立又常常转化为函数研究最值问题,本题中还要注意做题的严密性,等号不能丢掉。
例7.(2008福建卷,理12)已知函数y=f(x),y=g(x)的导函数的图象如下图,那么y=f(x),y=g(x)的图象可能是( )
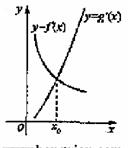
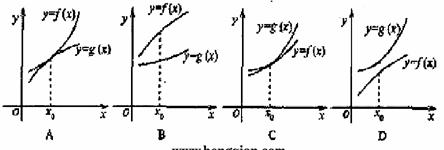
分析:注意观察导函数的图象以及原函数的图象,并把所得到的信息转化为原函数的信息,加以排除选择。
解:令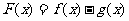 ,则
,则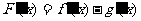 ,当
,当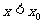 时,由图象知
时,由图象知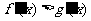 ,即
,即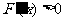 ,
,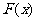 是增函数,则答案A,C错, 当
是增函数,则答案A,C错, 当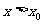 时,
时,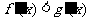 ,即
,即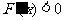 ,
,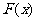 是减函数,则答案B错,故选D.
是减函数,则答案B错,故选D.
答案:D
评注:对于由图形给出的信息要从中提炼出来,并适当地用数学语言表述准确,本题中的两个函数可以转化为一个函数,进行构造,导函数的正负转化为原函数的增减。
3.转化函数关系
例5.(2008山东卷,文15)已知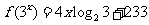 ,
,
则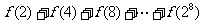 的值等于
.
的值等于
.
分析:本题中的函数不是以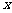 为整体,而是以
为整体,而是以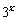 为整体给出的解析式,所以要求函数值,需要先求关于
为整体给出的解析式,所以要求函数值,需要先求关于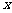 的解析式,再代入求值。
的解析式,再代入求值。
解:∵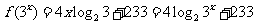 ,∴
,∴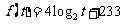 ,
,
则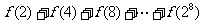
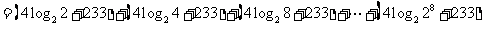
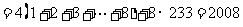
评注:有些题目中往往所给的解析式不是关于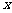 的解析式,这时需要我们把解析式进行转化,本题中先把函数进行转化,然后进行运算。
的解析式,这时需要我们把解析式进行转化,本题中先把函数进行转化,然后进行运算。
2.新定义运算转化为普通运算
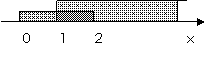
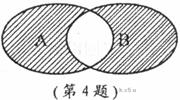 例3.(2008山东省泰安市)如图所示的韦恩图中,A、B是非空集合,定义集合A#B为阴影部分表示的集合.若
例3.(2008山东省泰安市)如图所示的韦恩图中,A、B是非空集合,定义集合A#B为阴影部分表示的集合.若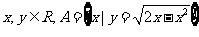 ,
,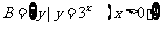 ,
则A#B为(
)
,
则A#B为(
)
A.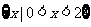 B.
B.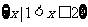
C.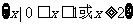 D.
D.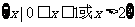
分析:根据图形语言可知定义的A#B转化为原有的运算应该是表示为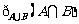 ,所以需要求出
,所以需要求出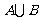 和
和 ,借助数轴求出并集与交集。
,借助数轴求出并集与交集。
 解:
解: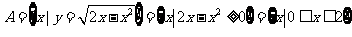 ,
,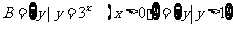 ,则
,则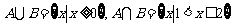 ,根据新运算,得A#B=
,根据新运算,得A#B=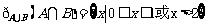 故选D
故选D
答案:D
评注:本题是集合中的新定义运算题,综合考查了图形语言、集合的描述法表示,函数的定义域和值域,以及集合的交并补的运算。解题的关键是由图形语言把新定义运算转化为原有的普通运算解出。
例4.(2008山东省郓城一中)定义一种运算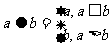 ,令
,令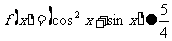 ,且
,且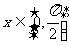 ,则函数
,则函数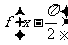 的最大值是( )
的最大值是( )
A.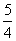 B.1 C.
B.1 C.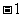 D.
D.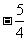
分析:根据新定义,知要确定函数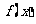 的解析式,需要比较
的解析式,需要比较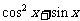 与
与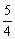 的大小关系,即需要求
的大小关系,即需要求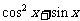 的取值范围,另外,还要注意自变量的取值范围,再确定
的取值范围,另外,还要注意自变量的取值范围,再确定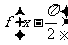 的解析式,从而求出函数的最大值。
的解析式,从而求出函数的最大值。
解:设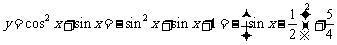 ,
,
∵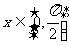 ,∴
,∴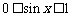 ,∴
,∴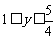 ,即
,即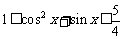 ,
,
根据新定义的运算可知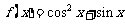 ,
,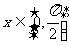
∴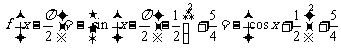 (
(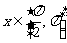 )
)
∴函数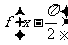 的最大值是
的最大值是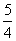 ,故选A
,故选A
答案:A
评注:解决新定义问题,首先要把定义读懂理解透,把陌生的新内容转化为熟悉的已知的内容,在此基础上进一步研究熟悉的问题。
1. 转化运算.
例1.若动直线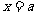 与函数
与函数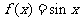 和
和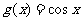 的图像分别交于
的图像分别交于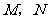 两点,则
两点,则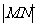 的最大值为( )
的最大值为( )
A.1 B.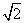 C.
C.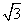 D.2
D.2
分析: 动直线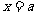 与函数
与函数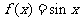 和
和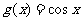 的图像分别交于
的图像分别交于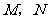 两点, 横坐标相同,那么
两点, 横坐标相同,那么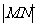 就是纵坐标之差,即
就是纵坐标之差,即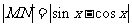 求最值。
求最值。
解: 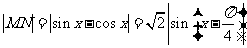 最大值为
最大值为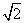
评注:审题要审准,读懂题意,将问题学会转化。
例2.(2008湖北卷,理14)已知函数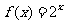 ,等差数列
,等差数列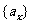 的公差为
的公差为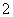 .若
.若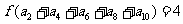 ,则
,则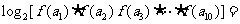 .
.
分析:题目中的已知条件很容易求得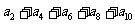 ,而所求的为
,而所求的为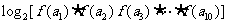 可以转化为等差数列
可以转化为等差数列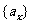 的前10项之和,根据公差,可以把前10项之和转化为用
的前10项之和,根据公差,可以把前10项之和转化为用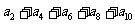 表示出来,从而求得。
表示出来,从而求得。
解:由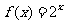 和
和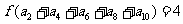 知
知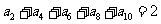 ,
,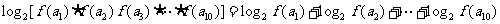
=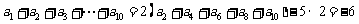
评注:仔细分析题目,把运算进行转化,可以大大地节省时间,提高做题的效率。本题中把等差数列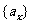 的前10项之和转化为用
的前10项之和转化为用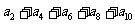 表示出来,比较快捷,减少计算量。
表示出来,比较快捷,减少计算量。
[例6]数列{an},a1=1,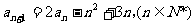
(1)求a2,a3的值;
(2)是否存在常数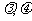 ,使得数列
,使得数列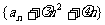 是等比数列,若存在,求出
是等比数列,若存在,求出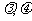 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)设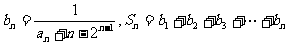 ,
,
证明:当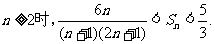
命题意图:数列的综合问题主要考点是数列、导数、不等式、数学归纳法,重点是综合、灵活运用数学知识分析、解决问题的能力,充分体现考生的综合数学素质。
解:(1)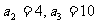
(2)设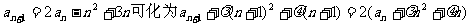 ,
,
即

故

∴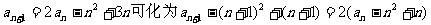
又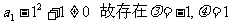 使得数列
使得数列
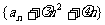 是等比数列
是等比数列
(3)证明:由(1)得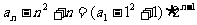
∴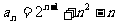 ,故
,故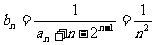
∵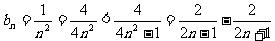
∴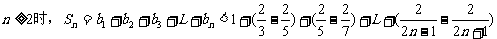
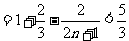 ,现证
,现证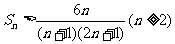
当n=2时,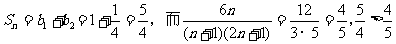 ,
,
故n=2时不等式成立,当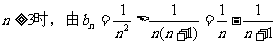 得
得

∵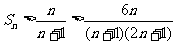
评注:数列解答题的命题热点是与不等式交汇,主要是呈现递推关系的综合性试题,其中,以函数与数列、不等式为命题载体,有着高等数学背景的数列解答题是未来高考命题的一个新的亮点,而命题的冷门则是数列的应用性解答题.
跟踪训练6.(本小题满分12分)在直角坐标平面上有一点列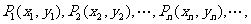 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数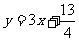 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以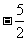 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,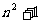 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求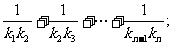
(3)设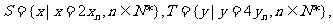 等差数列
等差数列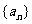 的任一项
的任一项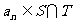 ,其中
,其中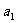 是
是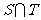 中的最大数,
中的最大数,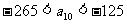 ,求数列
,求数列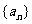 的通项公式.
的通项公式.
[例5]已知抛物线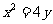 ,过定点
,过定点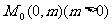 的直线
的直线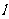 交抛物线于A、B两点.
交抛物线于A、B两点.
(Ⅰ)分别过A、B作抛物线的两条切线,A、B为切点,求证:这两条切线的交点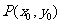 在定直线
在定直线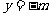 上.
上.
(Ⅱ)当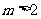 时,在抛物线上存在不同的两点P、Q关于直线
时,在抛物线上存在不同的两点P、Q关于直线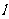 对称,弦长|PQ|中是否存在最大值?若存在,求其最大值(用
对称,弦长|PQ|中是否存在最大值?若存在,求其最大值(用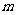 表示),若不存在,请说明理由.
表示),若不存在,请说明理由.
命题意图:圆锥曲线的综合问题主要考点是双曲线、抛物线、椭圆相结合,重点是圆锥曲线
的统一定义,点、弦、面积、取值范围、定值,函数与方程思想、数形结合思想。
[分析及解](Ⅰ)由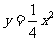 ,得
,得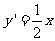 ,设
,设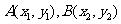
过点A的切线方程为: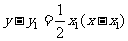 ,即
,即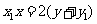
同理求得过点B的切线方程为: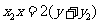
∵直线PA、PB过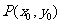 ,∴
,∴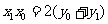 ,
,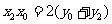
∴点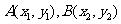 在直线
在直线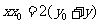 上,∵直线AB过定点
上,∵直线AB过定点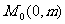 ,
,
∴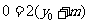 ,即
,即 ∴两条切线PA、PB的交点
∴两条切线PA、PB的交点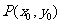 在定直线
在定直线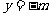 上.
上.
(Ⅱ) 设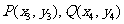 ,设直线
,设直线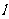 的方程为:
的方程为: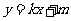 ,
,
则直线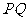 的方程为:
的方程为: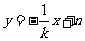 ,
,
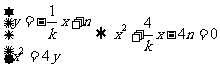 ,
,
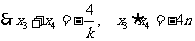 ,
,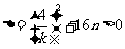 ①
①
设弦PQ的中点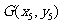 ,则
,则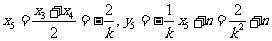
∵弦PQ的中点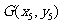 在直线
在直线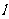 上,∴
上,∴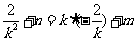 ,
,
即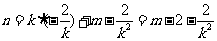 ②
②
②代入①中,得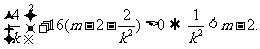 ③
③
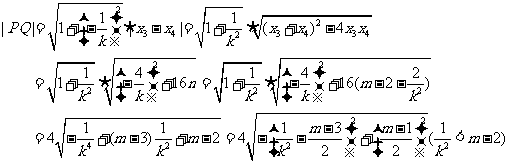
由已知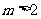 ,当
,当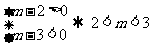 时,
弦长|PQ|中不存在最大值.
时,
弦长|PQ|中不存在最大值.
当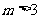 时,这时
时,这时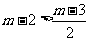 ,此时,弦长|PQ|中存在最大值,
,此时,弦长|PQ|中存在最大值,
即当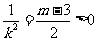 时,弦长|PQ|中的最大值为
时,弦长|PQ|中的最大值为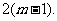
评注:圆锥曲线的试题涉及到函数、方程、导数、不等式、三角、向量、数列等各章节的知识,常把代数、三角、向量、数列、导数等知识交汇在一起成为典型题。而求曲线方程、弦长、角、面积、最值、轨迹、参数的值或取值范围,证明某种关系、证明定值、探索型、存在性讨论等问题是常考的题型,具有一定的综合性和灵活性,计算也较复杂,需要有较强的综合能力。解题中需用到函数与方程思想、分类讨论思想、数形结合思想、转化与划归思想。
跟踪训练5.(本小题满分12分)
已知椭圆C: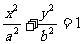 (a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,
(a>b>0),点F1、F2分别是椭圆的左、右焦点,点P(2,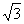 )在直线x=
)在直线x=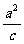 上,且|F1F2|=|PF2|,直线
上,且|F1F2|=|PF2|,直线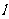 :y=kx+m为动直线,且直线
:y=kx+m为动直线,且直线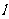 与椭圆C交于不同的两点A、B。
与椭圆C交于不同的两点A、B。
(Ⅰ)求椭圆C的方程;
(Ⅱ)若在椭圆C上存在点Q,满足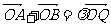 (O为坐标原点),求实数
(O为坐标原点),求实数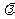 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当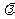 取何值时,△ABO的面积最大,并求出这个最大值.
取何值时,△ABO的面积最大,并求出这个最大值.
[例4]已知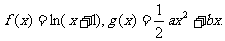
(1)若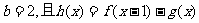 存在单调递减区间,求
存在单调递减区间,求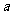 的取值范围;
的取值范围;
(2)若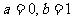 时,求证
时,求证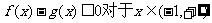 成立;
成立;
(3)利用(2)的结论证明:若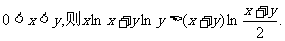
命题意图:函数与导数的综合问题主要考点是函数、导数、单调性、极值、切线、不等式,重点是三次或含自然对数的函数的导数、单调性、极值、切线、不等式(主要是恒成立、能成立或利用导数证明不等式问题)。属高档题的范畴,考查交汇知识综合处理能力。解题中需用到函数与方程思想、分类讨论思想、数形结合思想、转化与划归思想
[分析及解](1)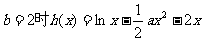
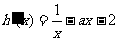 ,
,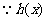 有单调减区间,∴
有单调减区间,∴
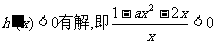 有解
有解
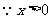 ,
∴
,
∴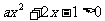 有解
有解
①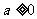 时合题意
时合题意
②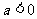 时,
时, ,即
,即 ,
∴
,
∴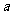 的范围是
的范围是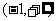
(2)设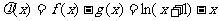 ,
,
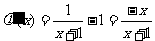 ,
,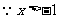
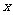 |
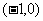 |
0 |
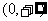 |
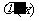 |
+ |
0 |
- |
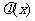 |
 |
最大值 |
 |
∴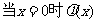 有最大值0,∴
有最大值0,∴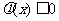 恒成立
恒成立
即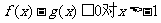 成立
成立
(3)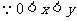
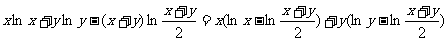
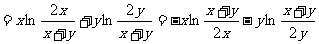
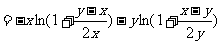
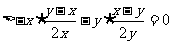 ,∴
,∴ 求证成立
求证成立
评注:导数是研究函数的工具,导数进入新教材之后,给函数问题注入了生机和活力,开辟了许多解题新途径,拓展了高考对函数问题的命题空间。所以把导数与函数综合在一起是顺理成章的事情,对函数的命题已不再拘泥于一次函数,二次函数,反比例函数,指数函数,对数函数等,对研究函数的目标也不仅限于求定义域,值域,单调性,奇偶性,对称性,周期性等,而是把高次多项式函数,分式函数,指数型,对数型函数,以及初等基本函数的和、差、积、商都成为命题的对象,试题的命制往往融函数,导数,不等式,方程等知识于一体,通过演绎证明,运算推理等理性思维,解决单调性,极值,最值,切线,方程的根,参数的范围等问题,这类题难度很大,综合性强,内容新,背景新,方法新,是高考命题的丰富宝藏。通过构造函数,以导数为工具,证明不等式,解题技巧是构造辅助函数,把不等式的证明转化为利用导数研究函数的单调性或求最值,从而证得不等式,而如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键。
跟踪训练4.(本小题满分12分)已知函数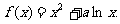
(I)当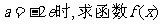 的单调区间和极值;
的单调区间和极值;
(II)若函数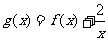 在[1,4]上是减函数,求实数a的取值范围.
在[1,4]上是减函数,求实数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com