
1.(2009福建省)为了得到函数y= 的图象,可以将函数y=sin2x的图象( )
的图象,可以将函数y=sin2x的图象( )
A.向左平移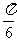 个单位长度,再向下平移
个单位长度,再向下平移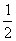 个单位长度
个单位长度
B.向右平移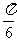 个单位长度,再向上平移
个单位长度,再向上平移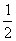 个单位长度
个单位长度
C.向左平移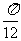 个单位长度,再向下平移
个单位长度,再向下平移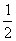 个单位长度
个单位长度
D.向右平移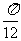 个单位长度,再向上平移
个单位长度,再向上平移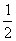 个单位长度
个单位长度
答案 D
2009年联考题
19.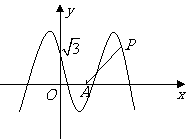 (2007江西)如图,函数
(2007江西)如图,函数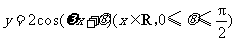 的图象与
的图象与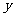 轴交于点
轴交于点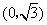 ,且在该点处切线的斜率为
,且在该点处切线的斜率为 .
.
(1)求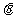 和
和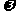 的值;
的值;
(2)已知点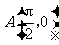 ,点
,点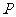 是该函数图象上一点,点
是该函数图象上一点,点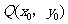 是
是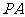 的中点,当
的中点,当 ,
, 时,求
时,求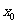 的值.
的值.
解:(1)将 ,
,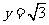 代入函数
代入函数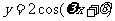 得
得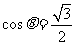 ,
,
因为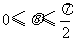 ,所以
,所以 .
.
又因为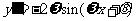 ,
,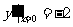 ,
, ,所以
,所以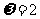 ,
,
因此 .
.
(2)因为点 ,
,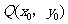 是
是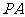 的中点,
的中点, ,
,
所以点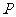 的坐标为
的坐标为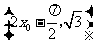 .
.
又因为点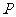 在
在 的图象上,所以
的图象上,所以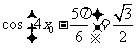 .
.
因为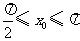 ,所以
,所以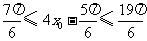 ,
,
从而得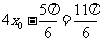 或
或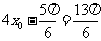 .
.
即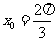 或
或 .
.
18.(2007湖北)已知函数 ,
,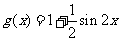 .
.
(I)设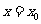 是函数
是函数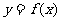 图象的一条对称轴,求
图象的一条对称轴,求 的值.
的值.
(II)求函数 的单调递增区间.
的单调递增区间.
解:(I)由题设知 .
.
因为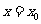 是函数
是函数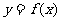 图象的一条对称轴,所以
图象的一条对称轴,所以
 ,
,
即 (
( ).
).
所以 .
.
当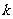 为偶数时,
为偶数时, ,
,
当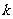 为奇数时,
为奇数时, .
.
(II)

 .
.
当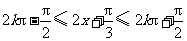 ,即
,即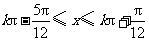 (
( )时,
)时,
函数 是增函数,
是增函数,
故函数 的单调递增区间是
的单调递增区间是 (
( ).
).
17.(2008广东)已知函数 ,
,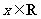 的最大值是1,其图像经过点
的最大值是1,其图像经过点 .
.
(1)求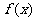 的解析式;
的解析式;
(2)已知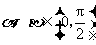 ,且
,且 ,
, ,求
,求 的值.
的值.
解(1)依题意有 ,则
,则 ,将点
,将点 代入得
代入得 ,
,
而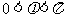 ,
, ,
, ,故
,故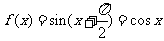 ;
;
(2)依题意有 ,而
,而 ,
,
 ,
,

16.(2008山东)已知函数f(x)=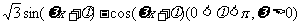 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为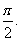
(Ⅰ)求f(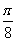 )的值;
)的值;
(Ⅱ)将函数y=f(x)的图象向右平移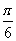 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
解(Ⅰ)f(x)=
=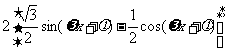
=2sin(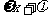 -
-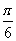 )
)
因为f(x)为偶函数,
所以对x∈R,f(-x)=f(x)恒成立,
因此sin(-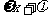 -
-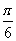 )=sin(
)=sin(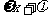 -
-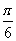 ).
).
即-sin cos(
cos(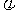 -
-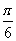 )+cos
)+cos sin(
sin(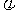 -
-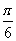 )=sin
)=sin cos(
cos(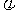 -
-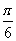 )+cos
)+cos sin(
sin(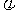 -
-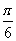 ),
),
整理得 sin cos(
cos(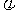 -
-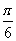 )=0.因为
)=0.因为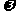 >0,且x∈R,所以cos(
>0,且x∈R,所以cos(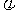 -
-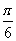 )=0.
)=0.
又因为0<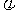 <π,故
<π,故 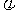 -
-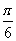 =
= .所以f(x)=2sin(
.所以f(x)=2sin( +
+ )=2cos
)=2cos .
.
由题意得 ,所以
,所以
故 f(x)=2cos2x.
因为

(Ⅱ)将f(x)的图象向右平移个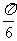 个单位后,得到
个单位后,得到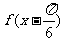 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到 的图象.
的图象.
所以
当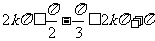 (k∈Z),
(k∈Z),
即4kπ+≤ ≤x≤4kπ+
≤x≤4kπ+ (k∈Z)时,g(x)单调递减.
(k∈Z)时,g(x)单调递减.
因此g(x)的单调递减区间为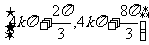 (k∈Z)
(k∈Z)
15.(2007四川)下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是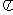 .
.
②终边在y轴上的角的集合是{a|a=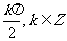 }.
}.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数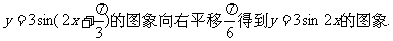
⑤函数
其中真命题的序号是
答案 ① ④
14.(2007安徽)函数 的图象为
的图象为 ,如下结论中正确的是__________(写出所有正确结论的编号).
,如下结论中正确的是__________(写出所有正确结论的编号).
①图象 关于直线
关于直线 对称;
对称;
②图象 关于点
关于点 对称;
对称;
③函数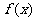 在区间
在区间 内是增函数;
内是增函数;
④由 的图角向右平移
的图角向右平移 个单位长度可以得到图象
个单位长度可以得到图象
答案 ①②③
13.(广东理科卷)已知函数 ,
,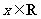 ,则
,则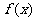 的最小正周期是
.
的最小正周期是
.
解析  ,所以函数的最小正周期
,所以函数的最小正周期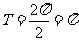 。
。
答案:
12.(2008江苏卷) 的最小正周期为
的最小正周期为 ,其中
,其中 ,则
,则
解析 本小题考查三角函数的周期公式。
答案:10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com