
1、函数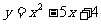 在区间
在区间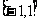 上的最大值与最小值
上的最大值与最小值
3、在解决实际应用问题中,关键在于建立数学模型和目标函数;如果函数在区间内只有一个极值点,那么根据实际意义判断是最大值还是最小值即可,不必再与端点的函数值进行比较。
2、函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个。
1、闭区间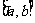 上的连续函数一定有最值;开区间
上的连续函数一定有最值;开区间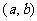 内的可导函数
内的可导函数
不一定有最值,若有唯一的极值,则此极值必是函数的最值。
解:先求导数,得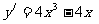
令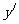 =0即
=0即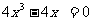 解得
解得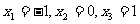
导数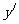 的正负以及
的正负以及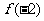 ,
,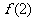 如下表
如下表
|
X |
-2 |
(-2,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1,2) |
2 |
|
y/ |
|
|
0 |
+ |
0 |
- |
0 |
+ |
|
|
y |
13 |
|
4 |
|
5 |
|
4 |
|
13 |
从上表知,当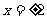 时,函数有最大值13,当
时,函数有最大值13,当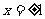 时,函数有最小值4
时,函数有最小值4
在日常生活中,常常会遇到什么条件下可以使材料最省,时间最少,效率最高等问题,这往往可以归结为求函数的最大值或最小值问题。
例2 用边长为60CM的正方形铁皮做一个无盖的水箱,先在四个角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成,问水箱底边的长取多少时,水箱容积最大,最大容积是多少?
例3、已知某商品生产成本C与产量P的函数关系为C=100+4P,价格R与产量P的函数关系为R=25-0.125P,求产量P为何值时,利润L最大。
3、将函数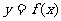 在
在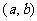 内的极值与
内的极值与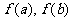 比较,其中最大的一个为最大值 ,最小的一个为最小值
比较,其中最大的一个为最大值 ,最小的一个为最小值
2、求函数 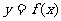 在
在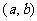 内的极值
内的极值
|
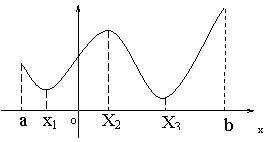 在某些问题中,往往关心的是函数在一个定义区间上,哪个值最大,哪个值最小
在某些问题中,往往关心的是函数在一个定义区间上,哪个值最大,哪个值最小
观察下面一个定义在区间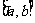 上的函数
上的函数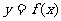 的图象
的图象
发现图中____________是极小值,_________是极大值,在区间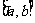 上的函数
上的函数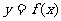
的最大值是______,最小值是_______
在区间 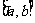 上求函数
上求函数 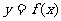 的最大值与最小值 的步骤:
的最大值与最小值 的步骤:
1、函数 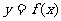 在
在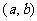 内有导数 ;
内有导数 ;
3、求y=x3-27x的 极值。
1、 ;2、
;2、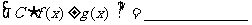
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com