6. 求下列函数的值域：

　 ; ;　 　;

5. 计算　　　 .

4. 函数(，且)的图象必经过点　　　　 .

3.　　　 若点既在函数的图象上，又在它的反函数的图象上，则=______，=_______

2. 函数的单调区间为　　　　 .

1.函数的定义域为　　　　 .，值域为　　　　 .

例1：已知＝，54^b＝3，用的值

解法1：由＝3得＝b

∴＝＝

解法2：由

设

所以

即：

所以

因此得：

例2、函数的定义域为　　　　 .

例3、函数的单调区间为　　　　 .

例4、已知函数.判断　的奇偶性并予以证明.

例5、按复利计算利息的一种储蓄，本金为元，每期利率为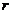，设本利和为元，存期为，写出本利和随存期变化的函数解析式. 如果存入本金1000元，每期利率为2.25%，试计算5期后的本利和是多少(精确到1元)？(复利是一种计算利息的方法，即把前一期的利息和本金加在一起算做本金，再计算下一期的利息. )

(小结：掌握指数函数、对数函数、幂函数的图象与性质，会用函数性质解决一些简单的应用问题. )

3. 比较下列各组中两个值的大小：；；

2.　　 求下列函数的定义域：；；

1.　　 提问：指数函数、对数函数、幂函数的图象和性质.