20．设a和b分别是先后抛掷一枚骰子得到的点数，且随机变量ξ表示方程的实根的个数(相等的两根算一个根)。

　 (1)求方程无实根的概率；

　 (2)求随机变量ξ的概率分布列；

　 (3)求在先后两次出现的点数中有4的条件下，方程有实根的概率。

19．已知的展开式的系数和大992。

　 求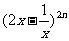的展开式中；(1)二项式系数最大的项；(2)系数的绝对值最大的项。

18．已知复数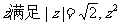的虚部为2。

　 (1)求复数z；

　 (2)设在复平面上的对应点分别为A，B，C，求△ABC的面积；

　 (3)若复数z在复平面内所对应的点位于第一象限，且复数m满足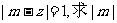的最值。

17．从集合，

求：(1)可以组成多少个双曲线？

　 (2)可以组成多少个焦点在x轴上的椭圆？

　 (3)可以组成多少个在区域内的椭圆？

16．对于集合N={1，2，3，…，n}的每一个非空子集，定义一个“交替和”如下：按照递减的次序重新排列该子集，然后从最大数开始交替地减、加后继的数。例如集合{1，2，4，6，9}的交替和是9-6+4-2+1=6，集合{5}的交替和为5。当集合N中的n=2时，集合N={1, 2}的所有非空子集为{1}，{2}，{1, 2}，则它的“交替和”的总和S₂=1+2+(2–1)=4，请你尝试对n=3、n=4的情况，计算它的“交替和”的总和S₃、S₄，并根据其结果猜测集合N={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和S_n=　　　　

14．设某种动物由出生算起活到10岁的概率为0.9，由出生算起活到15岁的概率为0.6，现有一个10岁的这种动物，它能活到15岁的概率是　　　 。

　 15．某城市在中心广场建造一个花圃(如图)，花圃分为5个

部分，现要将4种颜色的花全部种在花圃中，每部分种

一种颜色，且相邻部分的花不同色，则不同的栽种方法

共有　　　 种(用数字作答)。

13．将1，2，3填入3×3的方格中，要求每行、每列都没有重复数字，则不同的填写方法共有　　　　 种(用数字作答)。

12．已知随机变量X满足=　　　　 。

11．若多项式=　　　　 。

10．用1，2，3，4，5，6，7，8组成没有重复数字的八位数，要求1与2相邻，3与4上邻，5与6相邻，而7与8不相邻，这样的八位数共有　　　　 个(用数字作答)。