22. （本题满分12分）已知数列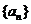满足：.

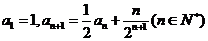  （3）在条件（2）下的椭圆方程，是否存在斜率为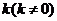的直线，与椭圆交于不同的两点A、B，满足，且使得过点Q，N（0，－1）两点的直线NQ满足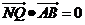？若存在，求出k的取值范围；若不存在，说明理由.

  （2）若直线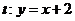与椭圆存在一个公共点E，使得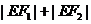取得最小值，求此最小值及此时椭圆的方程；

21. （本题满分12分）设椭圆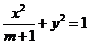的两个焦点是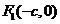与，且椭圆上存在点M，使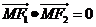. （1）求实数m 的取值范围；

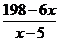
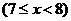
 （1）求总利润（利润＝销售额－成本）y（元）与销售价x（件）的函数关系式；

 （2）试问：当实际销售价为多少元时，总利润最大.

20. （本题满分12分）某种商品的成本为5元/ 件，开始按8元/件销售，销售量为50件，为了获得最大利润，商家先后采取了提价与降价两种措施进行试销。经试销发现：销售价每上涨1元每天销售量就减少10件；而降价后，日销售量Q（件）与实际销售价x（元）满足关系：