
科目:小学数学 来源: 题型:解答题
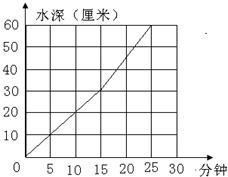 学校食堂有一个底面直径是60厘米,高80厘米的圆柱形水箱,水箱中装有A、B两个进水管,先开A管,过一段时间后两管同开,下面折线图表示进水情况,请根据图回答以下问题.
学校食堂有一个底面直径是60厘米,高80厘米的圆柱形水箱,水箱中装有A、B两个进水管,先开A管,过一段时间后两管同开,下面折线图表示进水情况,请根据图回答以下问题.科目:小学数学 来源: 题型:
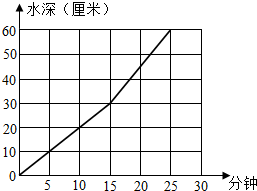 (2010?扬州)学校食堂有一个底面直径是60厘米,高80厘米的圆柱形水箱,水箱中装有A、B两个进水管,先开A管,过一段时间后两管同开,下面折线图表示进水情况,请根据图回答以下问题.
(2010?扬州)学校食堂有一个底面直径是60厘米,高80厘米的圆柱形水箱,水箱中装有A、B两个进水管,先开A管,过一段时间后两管同开,下面折线图表示进水情况,请根据图回答以下问题.科目:小学数学 来源: 题型:单选题
科目:小学数学 来源: 题型:
科目:小学数学 来源: 题型:
科目:小学数学 来源: 题型:
| 11 |
| 6 |
| 11 |
| 21 |
| 1月1日 | 2月1日 | 3月1日 | 4月1日 | |
| 水表读数(吨) | 90 | 110 | 135 | 165 |
| 电表读数(千瓦时) | 180 | 230 | 275 | 330 |
科目:小学数学 来源: 题型:阅读理解
科目:小学数学 来源: 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com