
| 双曲线与直线交于A、B两点,使反比例函数的值小于一次函数的值的x的取值范围是 |
|
| A.x>3 B.x<-2 C.-2<x<0或x>3 D.x<-2或0<x<3 |
科目:初中数学 来源: 题型:单选题
 双曲线与直线交于A、B两点,要使反比例函数的值小于一次函数的值,则x的取值范围是
双曲线与直线交于A、B两点,要使反比例函数的值小于一次函数的值,则x的取值范围是科目:初中数学 来源:福建省期中题 题型:单选题

科目:初中数学 来源: 题型:解答题
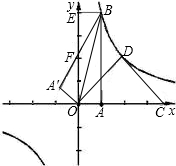
 图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.
图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.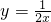 上是否存在点P,使点P到直线AB的距离最短的点,若存在,请求出点P的坐标及最短距离;若不存在,说明理由
上是否存在点P,使点P到直线AB的距离最短的点,若存在,请求出点P的坐标及最短距离;若不存在,说明理由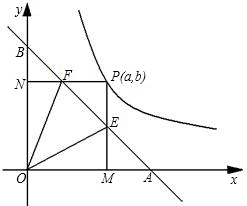
科目:初中数学 来源: 题型:
| k |
| x |
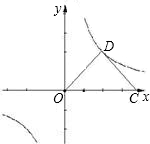
| k |
| x |
科目:初中数学 来源: 题型:解答题
 (k>0)上,点C在x轴的正半轴上且坐标为(4,0),△ODC是以CO为斜边的等腰直角三角形.
(k>0)上,点C在x轴的正半轴上且坐标为(4,0),△ODC是以CO为斜边的等腰直角三角形.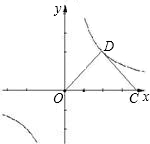

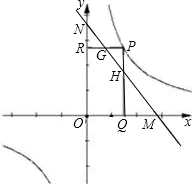
 (k>0)上的一动点,PQ⊥x轴于Q点,PR⊥y轴于R点,PQ,PR与直线MN交于H,G两点.给出下列两个结论:①△PGH的面积不变;②MG•NH的值不变,其中有且只有一个结论是正确的,请你选择并证明求值.
(k>0)上的一动点,PQ⊥x轴于Q点,PR⊥y轴于R点,PQ,PR与直线MN交于H,G两点.给出下列两个结论:①△PGH的面积不变;②MG•NH的值不变,其中有且只有一个结论是正确的,请你选择并证明求值.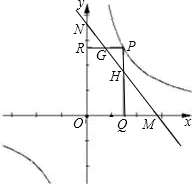
科目:初中数学 来源:不详 题型:解答题
| k |
| x |


| k |
| x |

科目:初中数学 来源: 题型:填空题
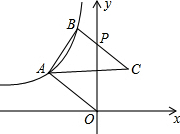 如图:已知反比例函数
如图:已知反比例函数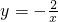 (x<0)和
(x<0)和 (x>0),直线OA与双曲线
(x>0),直线OA与双曲线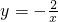 (x<0)交于A点,将直线OA向上平移使其分别交双曲线于B、C两点,与y轴交于P,且S△ABC=4,
(x<0)交于A点,将直线OA向上平移使其分别交双曲线于B、C两点,与y轴交于P,且S△ABC=4,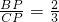 ,则k=________.
,则k=________.科目:初中数学 来源: 题型:解答题
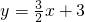 与x轴、y轴分别相交于A、B两点,与双曲线
与x轴、y轴分别相交于A、B两点,与双曲线 在第一象限
在第一象限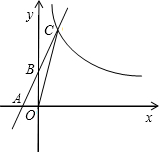 内交于点C,且S△AOC=6.
内交于点C,且S△AOC=6.科目:初中数学 来源: 题型:
 如图,Rt△ABO的顶点A是双曲线y=
如图,Rt△ABO的顶点A是双曲线y=| k |
| x |
| k |
| x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com