已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠ACB=∠EDF=90°，∠DEF=45°，AC=8cm，BC=6cm，EF=9cm．
如图（2），△DEF从图（1）的位置出发，以1cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2cm/s的速度沿BA向点A匀速移动．当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动、DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）连接PE，设四边形APEC的面积为y（cm²），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由；
（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

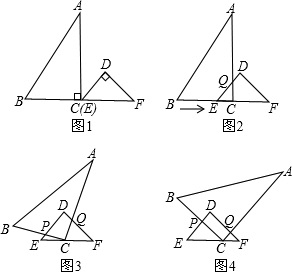已知：RT△ABC与RT△DEF中，∠ACB=∠EDF=90°，∠DEF=45°，EF=8cm，AC=16cm，BC=12cm．现将RT△ABC和RT△DEF按图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，并按如下方式运动．
运动一：如图2，△ABC从图1的位置出发，以1cm/s的速度沿EF方向向右匀速运动，DE与AC相交于点Q，当点Q与点D重合时暂停运动；
运动二：在运动一的基础上，如图3，RT△ABC绕着点C顺时针旋转，CA与DF交于点Q，CB与DE交于点P，此时点Q在DF上匀速运动，速度为

cm/s，当QC⊥DF时暂停旋转；
运动三：在运动二的基础上，如图4，RT△ABC以1cm/s的速度沿EF向终点F匀速运动，直到点C与点F重合时为止．
设运动时间为t（s），中间的暂停不计时，
解答下列问题
（1）在RT△ABC从运动一到最后运动三结束时，整个过程共耗时

s；
（2）在整个运动过程中，设RT△ABC与RT△DEF的重叠部分的面积为S（cm²），求S与t之间的函数关系式，并直接写出自变量t的取值范围；
（3）在整个运动过程中，是否存在某一时刻，点Q正好在线段AB的中垂线上，若存在，求出此时t的值；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

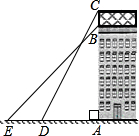已知：如图，一座商场大楼的顶部竖直立有一个矩形广告牌，小红同学在地面上选择了在一条直线上的三点A（A为楼底）、D、E，她在D处测得广告牌顶端C的仰角为60°，在E两处测得商场大楼楼顶B 的仰角为45°，DE=5米．已知，广告牌的高度BC=2.35米，求这座商场大楼的高度AB（

取1.73，

取1.41，小红的身高不计，结果保留整数）．

查看答案和解析>>

科目：初中数学 来源： 题型：

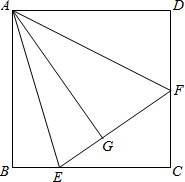已知，如图，正方形ABCD中，点E、F分别在边BC、CD上，且∠EAF=45°，AG⊥EF于G，EG=2，FG=3，求AG的边长．小萍同学灵活运用旋转的知识，将图形进行旋转变换，巧妙地解答了此题．请按照小萍的思路，探究并解答下列问题：
（1）把△ADF绕点A顺时针旋转90°，得△ABH，请在图中画出旋转后的图形；
（2）判断H、B、E三点是否在一条直线上，若在，请证明：△AEF≌△AEH；若不在，请说明理由；
（3）设AG=x，利用勾股定理，建立关于x的方程模型，求出x的值．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学

已知三点M、N、P不在同一条直线上，且MN=4厘米，NP=3厘米，M、P两点间的距离为x厘米，那么x的取值范围是________。