练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图示，AB+BC＞AC，其理由是三角形两边之和大于第三边


    A.正确
    B.错误
    A
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    11、如图所示，AB+BC＞AC，其理由是
    三角形任意两边之和大于第三边，任意两边之差小于第三边
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

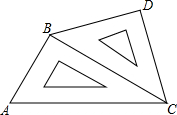    小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长．（两个三角板分别是等腰直角三角形和含30°的直角三角形）
    若已知CD=2，求AC的长．
    请你先阅读并完成解法一，然后利用锐角三角函数的知识写出与解法一不同的解法．
    解法一：在Rt△ABC中，∵BD=CD=2 
    ∴由勾股定理，BC=
    		22+22
    =2
    		2

    在Rt△ABC中，设AB=x
    ∵∠BCA=30°，∴AC=2AB=2x
    由勾股定理，AB2+BC2=AC2，即x2+(2
    		2
    )2=(2x)2
    ∵x＞0，解得x=
    2
    		6
    3
    2
    		6
    3
    ．∴AC=
    4
    		6
    3
    4
    		6
    3
    ．
    解法二：

    查看答案和解析>>

    科目：初中数学 来源：2009-2010学年天津市河西区九年级（上）期末数学试卷（解析版） 题型：解答题

    小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长．（两个三角板分别是等腰直角三角形和含30°的直角三角形）
    若已知CD=2，求AC的长．
    请你先阅读并完成解法一，然后利用锐角三角函数的知识写出与解法一不同的解法．
    解法一：在Rt△ABC中，∵BD=CD=2 
    ∴由勾股定理，BC=
    在Rt△ABC中，设AB=x
    ∵∠BCA=30°，∴AC=2AB=2x
    由勾股定理，AB2+BC2=AC2，即
    ∵x＞0，解得x=______

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    小明将一幅三角板如图所示摆放在一起，发现只要知道其中一边的长就可以求出其它各边的长．（两个三角板分别是等腰直角三角形和含30°的直角三角形）
    若已知CD=2，求AC的长．
    请你先阅读并完成解法一，然后利用锐角三角函数的知识写出与解法一不同的解法．
    解法一：在Rt△ABC中，∵BD=CD=2
    ∴由勾股定理，BC=数学公式
    在Rt△ABC中，设AB=x
    ∵∠BCA=30°，∴AC=2AB=2x
    由勾股定理，AB2+BC2=AC2，即数学公式
    ∵x＞0，解得x=________．∴AC=________．
    解法二：

    查看答案和解析>>

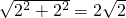
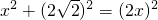
    科目：初中数学 来源：学习周报　数学　华师大八年级版　2009－2010学年　第16期　总第172期 题型：044

    阅读以下短文，然后解决下列问题：

    如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，那么称这样的矩形为三角形的“友好矩形”．如图所示，矩形ABEF即为△ABC的“友好矩形”．显然，当△ABC是钝角三角形时，其“友好矩形”只有一个．

    (1)仿照以上叙述，说明什么是一个三角形的“友好平行四边形”；

    (2)如图，若△ABC为直角三角形，且∠C＝90°，在图中画出△ABC的所有“友好矩形”，并比较这些矩形面积的大小；

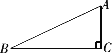
    (3)若△ABC是锐角三角形，且BC＞AC＞AB，在下图中画出△ABC的所有“友好矩形”，并指出其中周长最小的矩形．(不要求说明理由)

    查看答案和解析>>


    同步练习册答案