科目：初中数学 来源：不详 题型：解答题

如图，AB为的直径，点C在⊙O上，点P是直径AB上的一点(不与A，B重合)，过点P作AB的垂线交BC的延长线于点Q．
(1)在线段PQ上取一点D，使DQ=DC，连接DC，试判断CD与⊙O的位置关系，并说明理由．
(2)若cosB=，BP=6，AP=1，求QC的长．

查看答案和解析>>

科目：初中数学 来源：2013年山西省高级中等学校招生考试数学 题型：044

如图，AB为的直径，点C在⊙O上，点P是直径AB上的一点(不与A，B重合)，过点P作AB的垂线交BC的延长线于点Q．

(1)在线段PQ上取一点D，使DQ＝DC，连接DC，试判断CD与⊙O的位置关系，并说明理由．

(2)若cosB＝，BP＝6，AP＝1，求QC的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C，
（1）求证：CB∥PD；
（2）若BC=3，sin∠P=

3

5

，求⊙O的直径．

查看答案和解析>>

科目：初中数学 来源： 题型：

8、如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切，切点为D．如果∠A=35°，那么∠C等于（　　）

A、20°

B、30°

C、35°

D、55°

查看答案和解析>>

科目：初中数学 来源： 题型：

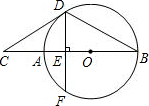如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，线段CD=10，连接BD．
（1）求证：∠CDE=2∠B；
（2）若BD：AB=

3

：2，求⊙O的半径及DF的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，AB是⊙O的直径，点C在⊙O上，∠BOC=108°，过点C作直线CD分别交直线AB和⊙O于点D、E，连接OE，DE=

1

2

AB，OD=2．
（1）求∠CDB的度数；
（2）我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比（或者底边长与腰长的比）等于黄金分割比

5 -1

2

．
①写出图中所有的黄金三角形，选一个说明理由；
②求弦CE的长；
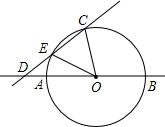③在直线AB或CD上是否存在点P（点C、D除外），使△POE是黄金三角形？若存在，画出点P，简要说明画出点P的方法（不要求证明）；若不存在，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D．若∠C=18°，则∠CDA=

 

度．

查看答案和解析>>

科目：初中数学 来源： 题型：

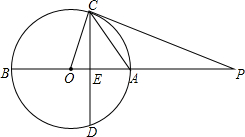如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB于点E，∠POC=∠PCE．
（1）求证：PC是⊙O的切线；
（2）若OE：EA=1：2，PA=6，求⊙O的半径；
（3）在（2）的条件下，求sin∠PCA的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

4、如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，DE∥BC，则图中与△ABC相似的三角形的个数为（　　）

A、4个

B、3个

C、2个

D、1个

查看答案和解析>>

科目：初中数学 来源： 题型：

12、如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D．若∠C=28°，则∠CDA=

121

度．

查看答案和解析>>