
科目:初中数学 来源:同步题 题型:解答题
科目:初中数学 来源:三点一测丛书八年级数学上 题型:044
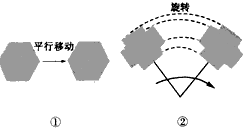
平移、对称与旋转是常见的几何变换,它们都是把一个几何图形F1变换成为一个几何图形F2,而且这种变换仅改变图形的位置,不改变图形的形状和大小.
例如:把△ABC沿直线BC平行移动,可以变到△ECD的位置(如图1);以BC为轴把△ABC翻折![]() ,可以变到△BDC的位置(如图2);绕A点把△ABC逆时针旋转
,可以变到△BDC的位置(如图2);绕A点把△ABC逆时针旋转![]() ,可以变到△AED的位置(如图3).
,可以变到△AED的位置(如图3).
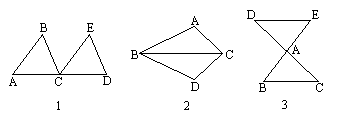
像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状大小的图形变换,叫做三角形的全等变换.
如图,在正方形ABCD中,E是AD的中点,F是BA的延长线上一点,AF=![]() AB.
AB.

(1)你认为可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置,怎样变化?
(2)根据全等变换的意义,你能否知道线段BE与DF之间的关系.
科目:初中数学 来源:2012年苏教版初中数学七年级下 11.2全等三角形练习卷(解析版) 题型:解答题
阅读下列材料:
如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;
如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;
如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.
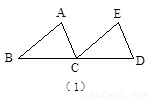

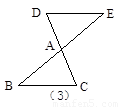
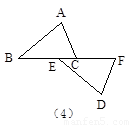
科目:初中数学 来源:2012年人教版八年级上第十一章全等三角形第一节全等三角形练习卷(解析版) 题型:解答题
(阅读与探究)如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.




科目:初中数学 来源: 题型:阅读理解
(阅读与探究)如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置,像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.




科目:初中数学 来源:同步题 题型:填空题
科目:初中数学 来源: 题型:022
(2)线段AB沿和它垂直的方向平移到A′B′,则线段AB和线段A′B′的关系是____________.
(3)△ABC平移到△DEF的位置,则△DEF和△ABC的关系是____________.
(4)平移只改变图形的____________,而不改变图形的____________.
科目:初中数学 来源:中华题王 数学 八年级上 (人教版) 人教版 题型:044
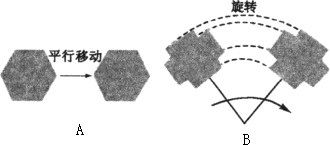
我们知道,对于两个图形,如果沿一条直线对折后,它们能完全重合,那么这两个图形成轴对称.既然成轴对称的两个图形能够完全重合,那么“关于某条直线对称的两个图形是全等形”.通常把图形从一种情况到另一种情况的对应关系称作图形变换,对称就是一种变换.观察图A、B容易看出,经过图形变换后,变换前后图形的位置改变了,但它的形状和大小并没有改变,这种只改变图形的位置,而不改变其形状、大小的图形变换叫做全等变换.前面说到的对称变换是一种全等变换;图A、B所示的变换分别是平移变换和旋转变换,它们都是全等变换(如图所示).
请你回答:全等变换的两个图形面积相等吗?为什么?
科目:初中数学 来源:三点一测丛书九年级数学上 题型:059
拿一张纸对折后,剪成两个全等的三角形,把这两个三角形一起放到图中△ABC的位置上.试一试,如果其中一个三角形不动,怎样移动另一个三角形,能够得到图中的各图形:
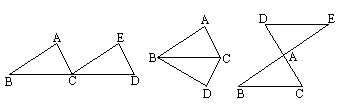
通过实际操作可以知道:(1)把△ABC沿直线BC移动线段BC那样长的距离,可以变到△ECD的位置;(2)以BC为轴把△ABC翻折![]() ,可以变到△DBC的位置;(3)以点A为中心,把△ABC旋转
,可以变到△DBC的位置;(3)以点A为中心,把△ABC旋转![]() ,可以变到△AED的位置.这些图形中的两个三角形之间有这样的关系,其中一个三角形是由另一个三角形按平行移动、翻折或旋转等方法得到的,像这样按一定方法把一个图形变成另一个图形叫做图形变换.
,可以变到△AED的位置.这些图形中的两个三角形之间有这样的关系,其中一个三角形是由另一个三角形按平行移动、翻折或旋转等方法得到的,像这样按一定方法把一个图形变成另一个图形叫做图形变换.
经过图形变换,图形的一些性质改变了,而另一些性质仍然保留下来.上面三个图形经过变换,图形的位置变化了,但形状大小都没有改变,即变换前后的图形全等,像这样只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换.
利用图形变换,可以为研究几何图形提供方便.
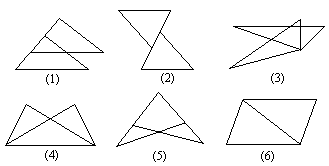
试一试,你能用两个全等三角形拼成图中的各种图形吗?这些图形都可以看成是一个三角形经过全等变换得到的.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com