| 如图，△ABC中，∠C=90°，AB=5，BC=4，点P是边BC 上的动点，则AP长不可能是 |
|
A．2.5 B．3 C．4 D．5 |
科目：初中数学 来源： 题型：
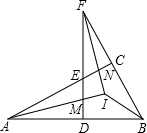如图，△ABC中，∠ACB=90°，D为AB上任一点，过D作AB的垂线，分别交边AC、BC的延长线于E、F两点，∠BAC、∠BFD的平分线交于点I，AI交DF于点M，FI交AC于点N，连接BI．下列结论：①∠BAC=∠BFD；②∠ENI=∠EMI；③AI⊥FI；④∠ABI=∠FBI；其中正确结论的个数是（ ）科目：初中数学 来源：2012届浙江省温州初中生学业考试数学试卷（带解析） 题型：解答题
如图，△ABC中，∠ACB=90°，D是边AB上的一点，且∠A=2∠DCB.E是BC上的一点，以EC为直径的⊙O经过点D。
【小题1】求证:AB是⊙O的切线；
【小题2】若CD的弦心距为1,BE=ED.求BD的长.
科目：初中数学 来源：2012年初中毕业升学考试（浙江温州卷）数学（带解析） 题型：解答题
如图，△ABC中，∠ACB=90°，D是边AB上的一点，且∠A=2∠DCB.E是BC上的一点，以EC为直径的⊙O经过点D。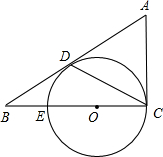
（1）求证:AB是⊙O的切线；
（2）若CD的弦心距为1,BE=EO.求BD的长.
科目：初中数学 来源：2013届四川德阳市中江县柏树中学九年级下学期第一次月考试数学试卷（带解析） 题型：解答题
如图，△ABC中，∠ACB=90°，D是边AB上一点，且∠A=2∠DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．
（1）求证：AB是⊙O的切线；
（2）若CD的弦心距为1，BE=EO，求BD的长．
科目：初中数学 来源：2013-2014学年湖北省大冶市九年级上学期期末考试数学试卷（解析版） 题型：解答题
如图，△ABC中，∠ACB=90°，D是边AB上一点，且∠A=2∠DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．
（1）求证：AB是⊙O的切线；
（2）若CD的弦心距为1，BE=EO，求BD的长．
科目：初中数学 来源：2012-2013学年四川德阳市九年级下学期第一次月考试数学试卷（解析版） 题型：解答题
如图，△ABC中，∠ACB=90°，D是边AB上一点，且∠A=2∠DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．
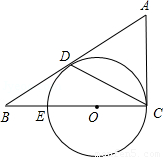
（1）求证：AB是⊙O的切线；
（2）若CD的弦心距为1，BE=EO，求BD的长．
科目：初中数学 来源：2011-2012学年浙江省生学业考试数学试卷（解析版） 题型：解答题
如图，△ABC中，∠ACB=90°，D是边AB上的一点，且∠A=2∠DCB.E是BC上的一点，以EC为直径的⊙O经过点D。
1.求证:AB是⊙O的切线；
2.若CD的弦心距为1,BE=ED.求BD的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
如图，△ABC中，∠B=90°，两直角边AB=7，BC=24，在三角形内有一点P到各边的距离相等，则这个距离是（ ）
如图，△ABC中，∠ACB=90°，D、E、F分别是边AB、AC、BC的中点，CD=3，试求EF的长度．
如图，△ABC中，AB=AC，D是BC的中点，∠A=90°，DE⊥AB，DF⊥AC，垂足分别为E、F．试说明四边形AEDF是正方形．