在比例式9:5=4:3x中.x=( )A.B.C.D.——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

在比例式9：5=4：3x中，x=（）

A.

相关习题

科目：初中数学 来源：上海专项题 题型：填空题

在比例式9：5=4：3x中，x=（）。

查看答案和解析>>

科目：初中数学 来源：2013年江苏省南京市玄武区中考一模数学试卷（带解析） 题型：解答题

在函数中，我们规定：当自变量增加一个单位时，因变量的增加量称为函数的平均变化率．例如，对于函数y＝3x＋1，当自变量x增加1时，因变量y＝3(x＋1)＋1＝3x＋4，较之前增加3，故函数y＝3x＋1的平均变化率为3．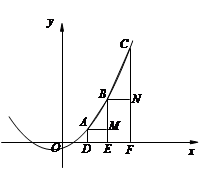

（1）①列车已行驶的路程s（km）与行驶的时间t（h）的函数关系式是s＝300t，该函数的平均变化率是；其蕴含的实际意义是；
②飞机着陆后滑行的距离y（m）与滑行的时间x（s）的函数关系式是y＝－1.5x2＋60x，求该函数的平均变化率；
（2）通过比较（1）中不同函数的平均变化率，你有什么发现；
（3）如图，二次函数y＝ax²＋bx＋c的图像经过第一象限内的三点A、B、C，过点A、B、C作x轴的垂线，垂足分别为D、E、F，AM⊥BE，垂足为M，BN⊥CF，垂足为N，DE＝EF，试探究△AMB与△BNC面积的大小关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

在函数中，我们规定：当自变量增加一个单位时，因变量的增加量称为函数的平均变化率．例如，对于函数y＝3x＋1，当自变量x增加1时，因变量y＝3(x＋1)＋1＝3x＋4，较之前增加3，故函数y＝3x＋1的平均变化率为3．

（1）①列车已行驶的路程s（km）与行驶的时间t（h）的函数关系式是s＝300t，该函数的平均变化率是 ▲ ；其蕴含的实际意义是 ▲ ；

②飞机着陆后滑行的距离y（m）与滑行的时间x（s）的函数关系式是y＝－1.5x²＋60x，求该函数的平均变化率；

（2）通过比较（1）中不同函数的平均变化率，你有什么发现；

（3）如图，二次函数y＝ax²＋bx＋c的图像经过第一象限内的三点A、B、C，过点A、B、C作x轴的垂线，垂足分别为D、E、F，AM⊥BE，垂足为M，BN⊥CF，垂足为N，DE＝EF，试探究△AMB与△BNC面积的大小关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

（1）①列车已行驶的路程s（km）与行驶的时间t（h）的函数关系式是s＝300t，该函数的平均变化率是；其蕴含的实际意义是；
②飞机着陆后滑行的距离y（m）与滑行的时间x（s）的函数关系式是y＝－1.5x2＋60x，求该函数的平均变化率；
（2）通过比较（1）中不同函数的平均变化率，你有什么发现；
（3）如图，二次函数y＝ax²＋bx＋c的图像经过第一象限内的三点A、B、C，过点A、B、C作x轴的垂线，垂足分别为D、E、F，AM⊥BE，垂足为M，BN⊥CF，垂足为N，DE＝EF，试探究△AMB与△BNC面积的大小关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

已知：A（m，2）是一次函数y=kx+b与反比例函数y=

（x＞0）的交点．
（1）求m的值；
（2）若该一次曲线的图象分别与x、y轴交于E、F两点，且点A恰为E、F的中点，求该直线的解析式；
（3）在y=

（x＞0）的图象上另取一点B，作BK⊥x轴于K，在（2）的条件下，在线段OF上取一点C，使FO=4CO．试问：在y轴上是否存在点P，使得△PCA和△PBK的面积相等？若存在，求出所有可能的点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

●探究：
（1）在图中，已知线段AB，CD，其中点分别为E，F．
①若A（-1，0），B（3，0），则E点坐标为

；
②若C（-2，2），D（-2，-1），则F点坐标为

；
（2）在图中，已知线段AB的端点坐标为A（a，b），B（c，d），求出图中AB中点D的坐标（用含a，b，c，d的代数式表示），并给出求解过程．
●归纳：
无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（a，b），B（c，d），AB中点为D（x，y）时，x=

，y=

．（不必证明）
●运用：
在图中，一次函数y=x-2与反比例函数y=

的图象交点为A，B．
①求出交点A，B的坐标；
②若以A，O，B，P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标．

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

●探究：
（1）在图中，已知线段AB，CD，其中点分别为E，F．
①若A（-1，0），B（3，0），则E点坐标为______；
②若C（-2，2），D（-2，-1），则F点坐标为______；
（2）在图中，已知线段AB的端点坐标为A（a，b），B（c，d），求出图中AB中点D的坐标（用含a，b，c，d的代数式表示），并给出求解过程．
●归纳：
无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（a，b），B（c，d），AB中点为D（x，y）时，x=______，y=______．（不必证明）
●运用：
在图中，一次函数y=x-2与反比例函数y=

的图象交点为A，B．
①求出交点A，B的坐标；
②若以A，O，B，P为顶点的四边形是平行四边形，请利用上面的结论求出顶点P的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，已知：A（m，2）是一次函数y=kx+b与反比例函数y=

的交点
（1）求m的值；
（2）若该一次函数分别与x轴y轴交于E、F两点，且直角△EOF的外心为点A．试求它的解析式；
（3）在y=

的图象上另取一点B，作BK⊥x轴于K，将（2）中的一次函数图象绕点A旋转后所得的直线记为l，若l与y轴的正半轴交于点C，且4CO=FO．试问：在y轴上是否存在点P，使得两个三角形的面积S_△PCA=S_△BOK？若存在，求点P的坐标，若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

（2013•玄武区一模）在函数中，我们规定：当自变量增加一个单位时，因变量的增加量称为函数的平均变化率．例如，对于函数y=3x+1，当自变量x增加1时，因变量y=3（x+1）+1=3x+4，较之前增加3，故函数y=3x+1的平均变化率为3．
（1）①列车已行驶的路程s（km）与行驶的时间t（h）的函数关系式是s=300t，该函数的平均变化率是

300

；其蕴含的实际意义是

列车的速度

；
②飞机着陆后滑行的距离y（m）与滑行的时间x（s）的函数关系式是y=-1.5x²+60x，求该函数的平均变化率；
（2）通过比较（1）中不同函数的平均变化率，你有什么发现；
（3）如图，二次函数y=ax²+bx+c的图象经过第一象限内的三点A、B、C，过点A、B、C作x轴的垂线，垂足分别为D、E、F，AM⊥BE，垂足为M，BN⊥CF，垂足为N，DE=EF，试探究△AMB与△BNC面积的大小关系，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

我们知道在平面直角坐标系中，二次函数y=-（x-1）²+2的图象可以由二次函数y=-x²的图象先向上平移2个单位，再向右平移1个单位得到．由此我们是否可以联想其它类型的函数也可以进行类似的平移呢？小明和小华两位同学对于这个问题进行了如下思考：
（1）现把一次函数y=-x的图象向上平移1个单位后得到一个新的函数的图象的解析式为

y=-x+1

；若再向右平移3个单位后的图象的解析式为

y=-x+4

．
（2）如果把反比例函数y=

的图象向上平移2个单位得反比例函数

的图象，若再向右平移2个单位后可以得到反比例函数

x-2

的图象；
（3）函数y=

2x+1

x+1

的图象可以由函数y=-

图象如何平移得到的；
（4）已知反比例函数y=

的图象将此函数向右平移2个单位后，再进行上下平移，使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形，求新函数的解析式．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学