
| 在同一平面直角坐标系中,对于函数①y=-x-1,②y=x+1,③y=-x+1,④y=-2(x+1)的图象,下列说法正确的是 |
A.通过点(-1,0)的是①③ B.交点在y轴上的是②④ C.相互平行的是①③ D.关于x轴对称的是②④ |
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| k |
| x |
 边形,求R点的坐标.
边形,求R点的坐标.科目:初中数学 来源:2012年福建省漳州市中考数学二模试卷 (解析版) 题型:解答题

科目:初中数学 来源:2012年江西省南昌市十五校第二次联考初三数学试卷(解析版) 题型:解答题

科目:初中数学 来源: 题型:解答题
 D上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P.
D上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P.科目:初中数学 来源: 题型:解答题
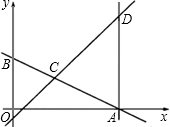
 x+5交x轴于点A,交y轴于点B,交直线y=x-1于点C.过点A作y轴的平行线交直线y=x-1于点D.点E为线段AD上一点,且tan∠DCE=
x+5交x轴于点A,交y轴于点B,交直线y=x-1于点C.过点A作y轴的平行线交直线y=x-1于点D.点E为线段AD上一点,且tan∠DCE= .点P从原点O出发沿OA边向点A匀速移动,同时,点Q从B点出发沿BO边向原点O匀速移动,点P与点Q同时到达A点和O点,设BQ=m.
.点P从原点O出发沿OA边向点A匀速移动,同时,点Q从B点出发沿BO边向原点O匀速移动,点P与点Q同时到达A点和O点,设BQ=m. 经过点C,R为y=
经过点C,R为y= 上一点,在整个移动过程中,若以P、Q、E、R为顶点的四边形是平行四
上一点,在整个移动过程中,若以P、Q、E、R为顶点的四边形是平行四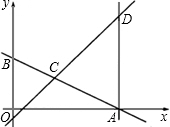 边形,求R点的坐标.
边形,求R点的坐标.科目:初中数学 来源:2011年黑龙江省哈尔滨市初中数学教师基本功大赛试卷(解析版) 题型:解答题
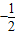 x+5交x轴于点A,交y轴于点B,交直线y=x-1于点C.过点A作y轴的平行线交直线y=x-1于点D.点E为线段AD上一点,且tan∠DCE=
x+5交x轴于点A,交y轴于点B,交直线y=x-1于点C.过点A作y轴的平行线交直线y=x-1于点D.点E为线段AD上一点,且tan∠DCE= .点P从原点O出发沿OA边向点A匀速移动,同时,点Q从B点出发沿BO边向原点O匀速移动,点P与点Q同时到达A点和O点,设BQ=m.
.点P从原点O出发沿OA边向点A匀速移动,同时,点Q从B点出发沿BO边向原点O匀速移动,点P与点Q同时到达A点和O点,设BQ=m. 经过点C,R为y=
经过点C,R为y=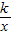 上一点,在整个移动过程中,若以P、Q、E、R为顶点的四边形是平行四边形,求R点的坐标.
上一点,在整个移动过程中,若以P、Q、E、R为顶点的四边形是平行四边形,求R点的坐标.
科目:初中数学 来源: 题型:
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x-2 |
| 3 |
| x-2 |
| 2x+1 |
| x+1 |
| 1 |
| x |
| 3 |
| x |
科目:初中数学 来源: 题型:解答题
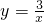 的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;
的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;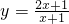 的图象可以由函数
的图象可以由函数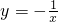 图象如何平移得到的;
图象如何平移得到的;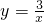 的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.
的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.科目:初中数学 来源:不详 题型:解答题
| 3 |
| x |
| 2x+1 |
| x+1 |
| 1 |
| x |
| 3 |
| x |
科目:初中数学 来源:2011-2012学年湘教版九年级(上)期末数学试卷(解析版) 题型:解答题
 的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;
的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象; 的图象可以由函数
的图象可以由函数 图象如何平移得到的;
图象如何平移得到的; 的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.
的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com