
| 如图,D、E分别是△ABC的AB、AC是的点,则下列条件不能判定△ADE与△ABC相似的是 |
|
A.∠B=∠ADE B.AD:AE=AB:AC C.AD:DE=AB:BC D.DE∥BC |
科目:初中数学 来源:不详 题型:单选题
| A.∠2=∠B | B.∠1=∠C | C.
| D.
|

科目:初中数学 来源:江苏期中题 题型:单选题

科目:初中数学 来源: 题型:
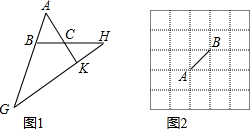 下列说法:
下列说法:科目:初中数学 来源: 题型:填空题
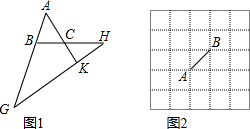 下列说法:
下列说法:科目:初中数学 来源:期末题 题型:单选题
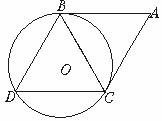
[ ]
 R2
R2 的两个圆只有一条公切线
的两个圆只有一条公切线科目:初中数学 来源:2013年初中毕业升学考试(四川乐山卷)数学(解析版) 题型:解答题
阅读下列材料:
如图1,在梯形ABCD中,AD∥BC,点M、N分别在边AB、BC上,且MN∥AD,记AD=a,BC=b,若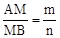 ,则有结论:
,则有结论: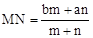 。
。
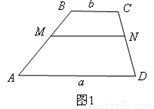
请根据以上结论,解答下列问题:

如图2,3,BE、CF是△ABC的两条角平分线,过EF上一点P分别作△ABC三边的垂线段PP1、PP2、PP3,交BC于点P1,交AB于点P2,交AC于点P3。
(1)若点P为线段EF的中点,求证:PP1=PP2+PP3;
(2)若点P在线段EF上任意位置时,试探究PP1、PP2、PP3的数量关系,给出证明。
科目:初中数学 来源:不详 题型:解答题
 ,则有结论:
,则有结论: 。
。

科目:初中数学 来源:期末题 题型:单选题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com