
科目:初中数学 来源: 题型:
 若不存在,请说明理由.
若不存在,请说明理由.科目:初中数学 来源: 题型:解答题
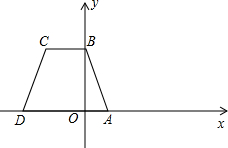 若不存在,请说明理由.
若不存在,请说明理由.科目:初中数学 来源:2002年江苏省泰州市中考数学试卷(解析版) 题型:解答题

科目:初中数学 来源:2012届福建省晋江市初中毕业班质量检查(二)数学卷(带解析) 题型:解答题
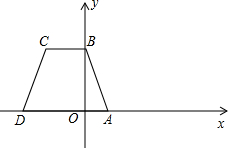
把一块三角板置于平面直角坐标系中,三角板的直角顶点为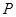 ,两直角边与
,两直角边与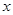 轴交于
轴交于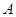 、
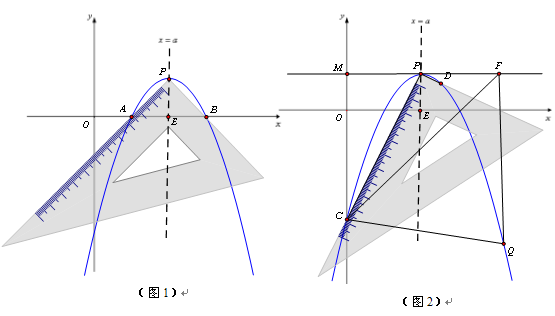
、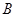 ,如图1,测得
,如图1,测得 ,
, .以
.以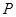 为顶点的抛物线
为顶点的抛物线 恰好经过
恰好经过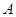 、
、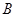 两点,抛物线的对称轴
两点,抛物线的对称轴 与
与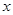 轴交于点
轴交于点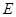 .
.
(1) 填空: ,
, ,点
,点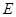 的坐标为 ;
的坐标为 ;
(2)设抛物线与 轴交于点
轴交于点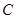 ,过
,过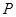 作直线
作直线 ⊥
⊥ 轴,垂足为
轴,垂足为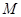 .如图2,把三角板绕着点
.如图2,把三角板绕着点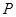 旋转一定角度,使其中一条直角边恰好过点
旋转一定角度,使其中一条直角边恰好过点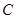 ,另一条直角边与抛物线的交点为
,另一条直角边与抛物线的交点为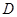 ,试问:点
,试问:点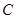 、
、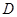 、
、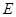 三点是否在同一直线上?请说明理由.
三点是否在同一直线上?请说明理由.
(3)在(2)的条件下,若 为抛物线上的一动点, 连结
为抛物线上的一动点, 连结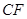 、
、 ,过
,过 作
作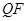 ⊥
⊥ ,垂足为
,垂足为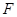 .试探索:是否存在点
.试探索:是否存在点 ,使得
,使得 是以
是以 为腰的等腰三角形?若存在,请求出
为腰的等腰三角形?若存在,请求出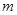 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:初中数学 来源:2011-2012学年福建省晋江市毕业班质量检查(二)数学卷(解析版) 题型:解答题
把一块三角板置于平面直角坐标系中,三角板的直角顶点为 ,两直角边与
,两直角边与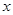 轴交于
轴交于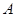 、
、 ,如图1,测得
,如图1,测得 ,
,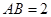 .以
.以 为顶点的抛物线
为顶点的抛物线 恰好经过
恰好经过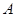 、
、 两点,抛物线的对称轴
两点,抛物线的对称轴 与
与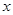 轴交于点
轴交于点 .
.

(1) 填空: ,
, ,点
,点 的坐标为
;
的坐标为
;
(2)设抛物线与 轴交于点
轴交于点 ,过
,过 作直线
作直线 ⊥
⊥ 轴,垂足为
轴,垂足为 .如图2,把三角板绕着点
.如图2,把三角板绕着点 旋转一定角度,使其中一条直角边恰好过点
旋转一定角度,使其中一条直角边恰好过点 ,另一条直角边与抛物线的交点为
,另一条直角边与抛物线的交点为 ,试问:点
,试问:点 、
、 、
、 三点是否在同一直线上?请说明理由.
三点是否在同一直线上?请说明理由.
(3)在(2)的条件下,若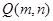 为抛物线上的一动点, 连结
为抛物线上的一动点, 连结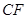 、
、 ,过
,过 作
作 ⊥
⊥ ,垂足为
,垂足为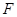 .试探索:是否存在点
.试探索:是否存在点 ,使得
,使得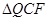 是以
是以 为腰的等腰三角形?若存在,请求出
为腰的等腰三角形?若存在,请求出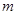 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:初中数学 来源:2001年全国中考数学试题汇编《二次函数》(02)(解析版) 题型:解答题

科目:初中数学 来源:2001年江苏省泰州市中考数学试卷(解析版) 题型:解答题

科目:初中数学 来源:北京同步题 题型:填空题




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com