练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在①(-3x-y)(3x+y)；②(-3x-y)(3x-y)；③(-3x+y)(3x-y)；④(-3x+y) (3x+y)这四个式子中，能利用平方差公式计算的是

    A．①②
    B．②③
    C．③④
    D．②④
    D
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：

    （1997•四川）已知一次函数y=kx+b的图象与另一个一次函数y=3x+2的图象相交于y轴上的点A，且x轴下方的一点B（3，n）在一次函数y=kx+b的图象上n满足关系式|n|=3-
    4n
    ．
    （1）求这个一次函数的解析式；
    （2）在直角坐标系内画出（1）题中函数的图象（要求列表、描点、连线）．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：单选题

    在①(-3x-y)(3x+y)；②(-3x-y)(3x-y)；③(-3x+y)(3x-y)；④(-3x+y) (3x+y)这四个式子中，能利用平方差公式计算的是
    [     ]
    A．①②
    B．②③
    C．③④
    D．②④

    查看答案和解析>>

    科目：初中数学 来源：2012届浙江省九年级毕业生学业考试模拟数学卷（解析版） 题型：选择题

     林老师给出一个函数，甲、乙、丙三位同学分别指出了这个函数的一个性质：甲：函数的图象经过第二象限；乙：函数的图象经过第四象限；丙：在每一个象限内，y值随x值增大而增大.根据他们的叙述，林老师给出的这个函数可能是（　▲　）

    A．y＝－3x                    B．y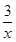＝－                       C．y＝x－3                    D．y＝x2－3

     

    查看答案和解析>>

    科目：初中数学 来源：月考题 题型：单选题

    在①6a2b=2a2·3b；②x2-4-3x=（x+2）（x-2）-3x；③ab2-2ab=ab（b-2）；④3x2-2x+1=x（3x-2+）这四个式子中，从左边到右边的变形，是因式分解的有
    [     ]
    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

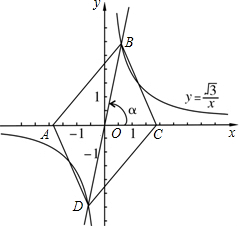    精英家教网我们容易发现：反比例函数的图象是一个中心对称图形．你可以利用这一结论解决问题．如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x轴所在的直线绕着原点O逆时针旋转α度角后的图形．若它与反比例函数y=
    		3
    x
    的图象分别交于第一、三象限的点B，D，已知点A（-m，O）、C（m，0）．
    （1）直接判断并填写：不论α取何值，四边形ABCD的形状一定是
     
    ；
    （2）①当点B为（p，1）时，四边形ABCD是矩形，试求p，α，和m的值；
    ②观察猜想：对①中的m值，能使四边形ABCD为矩形的点B共有几个？（不必说理）
    （3）试探究：四边形ABCD能不能是菱形？若能，直接写出B点的坐标，若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    我们容易发现：反比例函数的图象是一个中心对称图形．你可以利用这一结论解决问题．如图，在同一直角坐标系中，正比例函数的图象可以看作是：将x轴所在的直线绕着原点O逆时针旋转α度角后的图形．若它与反比例函数y=
    		3
    x
    的图象分别交于第一、三象限的点B，D，已知点A（-m，O）、C（m，0）．
    （1）直接判断并填写：不论α取何值，四边形ABCD的形状一定是______；
    （2）①当点B为（p，1）时，四边形ABCD是矩形，试求p，α，和m的值；
    ②观察猜想：对①中的m值，能使四边形ABCD为矩形的点B共有几个？（不必说理）
    （3）试探究：四边形ABCD能不能是菱形？若能，直接写出B点的坐标，若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源：模拟题 题型：解答题

    直线y=3x-3与x轴交于点A，与y轴交于点B，抛物线y=ax2+2ax+b经过A、B两点。
    （1）求这个二次函数的解析式；
    （2）将点B向右平移5个单位，再向上平移5个单位得到点C，问抛物线上是否存在点D、E，使以AC为边的四边形为平行四边形，若存在，求出D、E的坐标，若不存在，说明理由；
    （3）若N（-2，m）为抛物线上一点，P为抛物线上、直线AN下方一动点，当点P运动到什么位置时，△ANP的面积最大？求出此时P点的坐标和△ANP的最大面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线y=
    		3
    x+2
    		3
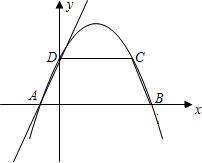    与x轴交于点A、与y轴交于点D，以AD为腰，以x轴为底作精英家教网等腰梯形ABCD（AB＞CD），且等腰梯形的面积是8
    		3
    ，二次函数y=ax2+bx+c经过等腰梯形的四个顶点．
    （1）求点A，B，C的坐标
    （2）求抛物线的解析式；
    （3）若点P为x轴上的一个动点，当点P运动到什么位置时，△ADP为等腰三角形，求这时点P的坐标；
    （4）若点P为抛物线上的一个动点，是否存在点P使△ADP为等腰三角形？若不存在，请说明理由；若存在，简要地进行说明有几个，并至少求出其中的一个点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解答题
    ①当m取何值时，关于x的方程：3x-2=4与5x-1=-m的解相等？
    ②一堆小麦用8个编织袋来装，以每袋55千克为标准，超过的记作为正数，不足的记作为负数，现记录如下：（单位：千克）
    +2，-3，+2，+1，-2，-1，0，-2
    （1）这堆小麦共重多少千克？
    （2）若每千克小麦的售价为1.2元，则这堆小麦可卖多少钱？
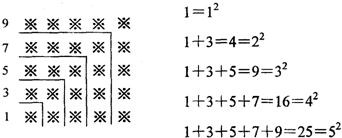
    ③探索规律：观察下面由“※”组成的图案和算式，解答问题：精英家教网
    （1）请猜想1+3+5+7+9+…+19=
     
    ；
    （2）请猜想1+3+5+7+9+…+（2n-1）+（2n+1）=
     
    ；
    （3）请用上述规律计算：103+105+107+…+2003+2005．
    ④在左边的日历中，用一个正方形任意圈出二行二列四个数，
    如精英家教网精英家教网
    若在第二行第二列的那个数表示为a，其余各数分别为b，c，d．
    如精英家教网
    （1）分别用含a的代数式表示b，c，d这三个数．
    （2）求这四个数的和（用含a的代数式表示，要求合并同类项化简）
    （3）这四个数的和会等于51吗？如果会，请算出此时a的值，如果不会，说明理由．（要求列方程解答）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    解答题
    ①当m取何值时，关于x的方程：3x-2=4与5x-1=-m的解相等？
    ②一堆小麦用8个编织袋来装，以每袋55千克为标准，超过的记作为正数，不足的记作为负数，现记录如下：（单位：千克）
    +2，-3，+2，+1，-2，-1，0，-2
    （1）这堆小麦共重多少千克？
    （2）若每千克小麦的售价为1.2元，则这堆小麦可卖多少钱？
    ③探索规律：观察下面由“※”组成的图案和算式，解答问题：
    （1）请猜想1+3+5+7+9+…+19=______；
    （2）请猜想1+3+5+7+9+…+（2n-1）+（2n+1）=______；
    （3）请用上述规律计算：103+105+107+…+2003+2005．
    ④在左边的日历中，用一个正方形任意圈出二行二列四个数，
    如
    若在第二行第二列的那个数表示为a，其余各数分别为b，c，d．
    如
    （1）分别用含a的代数式表示b，c，d这三个数．
    （2）求这四个数的和（用含a的代数式表示，要求合并同类项化简）
    （3）这四个数的和会等于51吗？如果会，请算出此时a的值，如果不会，说明理由．（要求列方程解答）

    查看答案和解析>>


    同步练习册答案