
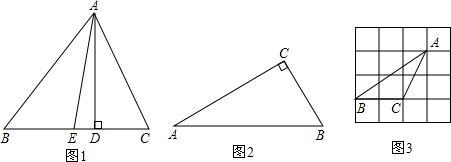
| 已知△ABC,有如下三种说法: (1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°  ∠A; ∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A; (3)如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-  ∠A. ∠A. |
|
| 上述说法正确的个数是 |
A.0 B.1 C.2 D.3 |
科目:初中数学 来源: 题型:

科目:初中数学 来源: 题型:
| DE | BE |
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源:辽宁省中考真题 题型:解答题
科目:初中数学 来源:2008-2009学年九年级数学期末综合测试(2)(解析版) 题型:解答题
科目:初中数学 来源:2006年辽宁省大连市旅顺口区中考数学试卷(课标卷)(解析版) 题型:解答题
科目:初中数学 来源: 题型:
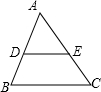 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质:| 1 | 2 |
科目:初中数学 来源: 题型:解答题
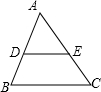 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质: BC;④DE∥BC.
BC;④DE∥BC.科目:初中数学 来源:期末题 题型:单选题
 ∠A;
∠A; ∠A.
∠A. 
科目:初中数学 来源:2006年辽宁省大连市旅顺口区初中毕业升学统一考试试题数学试卷 题型:059
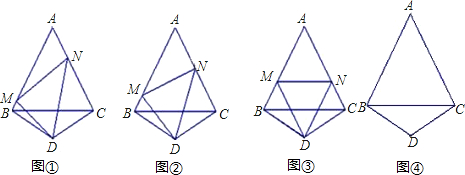
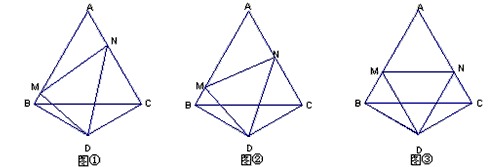
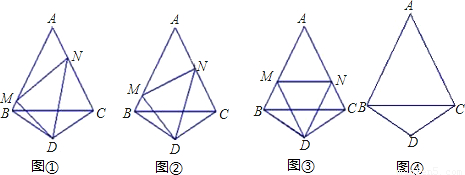
操作:如图,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.
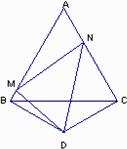
探究:线段BM、MN、NC之间的关系,并加以证明.
说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);
(2)在你经历说明(1)的过程之后,可以从下列①、②中选取一个补充或更换已知条件,完成你的证明.
注意:选取①完成证明得10分;选取②完成证明得5分.
①AN=NC(如图);
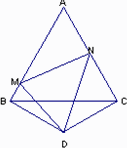
②DM∥AC(如图).
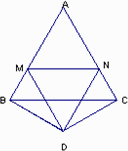
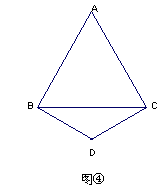
若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图中画出图形,并说明理由.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com