△ABC 中，AB边上的中线CD将△ABC分成两个等腰三角形，则∠ACB=_______度．

AB边上的中线CD将△ABC分成两个等腰三角形，则∠ACB=________度．

用两个全等的等边△ABC和△ADC，在平面上拼成菱形ABCD，把一个含60°角的三角尺与这个菱形重合，使三角尺有两边分别在AB、AC上，将三角尺绕点A按逆时针方向旋转
（1）如图1，当三角尺的两边与BC、CD分别相交于点E、F时，观察或测量BE，CF的长度，你能得出什么结论？证明你的结论．
（2）如图2，当三角尺的两边与BC、CD的延长线分别交于E、F时，你在（1）中的结论还成立吗？请说明理由．

已知四边形ABCD中，AB⊥AD，BC⊥CD，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN绕B点旋转，它的两边分别交AD，DC（或它们的延长线）于E、F，
（1）当∠MBN绕B点旋转到AE=CF时（如图1），试猜想AE，CF，EF之间存在怎样的数量关系？请将三条线段分别填入后面横线中：______+______=______（不需证明）
（2）当∠MBN绕B点旋转到AE≠CF时，在图2和图3这两种情况下，上问的结论分别是否仍然成立？若成立，请给出证明；若不成立，那么这三条线段又有怎样的数量关系？请写出你的猜想，不需证明．

如图①，点C将线段AB分成两部分，如果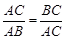，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S₁、S₂，如果，那么称直线l为该图形的黄金分割线．

1.研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图②所示，则直线CD是△ABC的黄金分割线．你认为对吗？为什么？

2.请你说明：三角形的中线是否也是该三角形的黄金分割线？

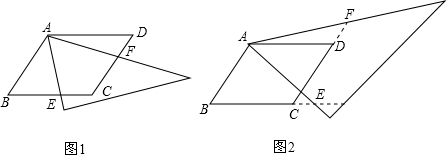
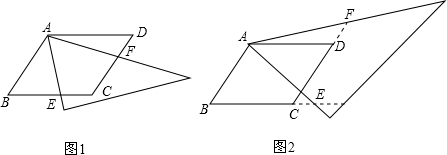
3.研究小组在进一步探究中发现：过点C任意作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF，如图③所示，则直线EF也是△ABC的黄金分割线．请你说明理由．

4.如图④，点E是□ABCD的边AB上的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是□ABCD的黄金分割线，请你画一条□ABCD的黄金分割线，使它不经过□ABCD各边黄金分割点．

如图①，点C将线段AB分成两部分，如果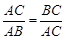，那么称点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S₁、S₂，如果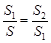，那么称直线l为该图形的黄金分割线．
【小题1】研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图②所示，则直线CD是△ABC的黄金分割线．你认为对吗？为什么？
【小题2】请你说明：三角形的中线是否也是该三角形的黄金分割线？
【小题3】研究小组在进一步探究中发现：过点C任意作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF，如图③所示，则直线EF也是△ABC的黄金分割线．请你说明理由．
【小题4】如图④，点E是□ABCD的边AB上的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是□ABCD的黄金分割线，请你画一条□ABCD的黄金分割线，使它不经过□ABCD各边黄金分割点．