
如图,A、B是反比例函数y= 上的两个点,AC⊥x轴于点C, BD⊥y轴交于点D,连接AD、BC,则△ABD与△ACB的面积大小关系是 上的两个点,AC⊥x轴于点C, BD⊥y轴交于点D,连接AD、BC,则△ABD与△ACB的面积大小关系是 |
|
A.  B.  C.  D.以上都有可能 |
科目:初中数学 来源: 题型:
| m |
| x |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
科目:初中数学 来源: 题型:
| k | x |
 BF的面积为4.
BF的面积为4.科目:初中数学 来源: 题型:解答题
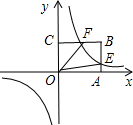
 图象的一支曲线经过矩形OABC的边AB、BC的中点E、F,且四边形OE
图象的一支曲线经过矩形OABC的边AB、BC的中点E、F,且四边形OE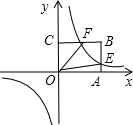 BF的面积为4.
BF的面积为4.科目:初中数学 来源: 题型:解答题
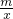 (x>0)的图象与一次函数y=-
(x>0)的图象与一次函数y=- x+
x+ 的图象交于A、B两点,点C的坐标为(1,
的图象交于A、B两点,点C的坐标为(1, ),连接AC,AC平行于y轴.
),连接AC,AC平行于y轴.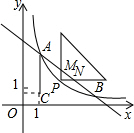
科目:初中数学 来源:中考真题 题型:解答题
 (k≠0)的图象经过点(-2,8)。
(k≠0)的图象经过点(-2,8)。
科目:初中数学 来源:内蒙古自治区中考真题 题型:解答题
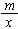 (x>0)的图象与一次函数
(x>0)的图象与一次函数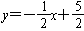 的图象交于A、B两点,点C的坐标为(1,
的图象交于A、B两点,点C的坐标为(1,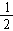 ),连接AC,AC∥y轴。
),连接AC,AC∥y轴。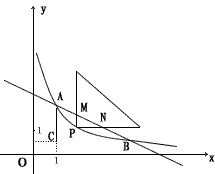
科目:初中数学 来源: 题型:
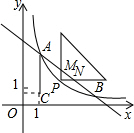
如图,已知反比例函数![]() (
(![]() )的图象与一次函数
)的图象与一次函数![]() 的图象交于
的图象交于![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() 平行于
平行于![]() 轴.
轴.
(1)求反比例函数的解析式及点![]() 的坐标.
的坐标.
(2)现有一个直角三角板,让它的直角顶点![]() 在反比例函数图象上的
在反比例函数图象上的![]() 之间的部分滑动(不与
之间的部分滑动(不与![]() 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于![]() 轴、
轴、![]() 轴,且与线段
轴,且与线段![]() 交于
交于![]() 两点,试判断
两点,试判断![]() 点在滑动过程中
点在滑动过程中![]() 是否与
是否与![]() 总相似,简要说明判断理由.
总相似,简要说明判断理由.
 |
科目:初中数学 来源: 题型:
如图,已知反比例函数![]() (k≠0)的图象经过点(-2,8).
(k≠0)的图象经过点(-2,8).
(1)求这个反比例函数的解析式;
(2)若(2,y1),(4,y2)是这个反比例函数图象上的两个点,请比较y1、y2的大小,并说明理由.

科目:初中数学 来源:2012年初中毕业升学考试(浙江湖州卷)数学(带解析) 题型:解答题
如图,已知反比例函数 (k≠0)的图象经过点(-2,8).
(k≠0)的图象经过点(-2,8).
(1)求这个反比例函数的解析式;
(2)若(2,y1),(4,y2)是这个反比例函数图象上的两个点,请比较y1、y2的大小,并说明理由.
科目:初中数学 来源:第1章《反比例函数》常考题集(17):1.3 实际生活中的反比例函数(解析版) 题型:解答题
 (x>0)的图象与一次函数y=-
(x>0)的图象与一次函数y=- x+
x+ 的图象交于A、B两点,点C的坐标为(1,
的图象交于A、B两点,点C的坐标为(1, ),连接AC,AC平行于y轴.
),连接AC,AC平行于y轴.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com