
| 如图所示,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE的两侧,BD⊥AE于D,AE⊥CE于E,DE=4cm,CE=2cm,则BD=( )cm。 |
|
A.2 B.4 C.6 D.8 |
科目:初中数学 来源:同步题 题型:填空题

科目:初中数学 来源: 题型:044
如图①所示,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE的同侧,BD⊥AE于D,CE⊥AE于E.
(1)请说明DE=BD+CE的理由;
(2)若直线AE绕A点旋转到图②位置时(BD>CE),其余条件不变,问DE与BD、 CE有怎样的数量关系?直接写出结果;
(3)若直线AE绕A点继续旋转到图③位置时,其余条件也不变,问DE与BD、CE的数量关系又如何?直接写出结果.

科目:初中数学 来源:数学教研室 题型:013
如图所示,在△ABC中,∠BAC=90°,AB=AC=2,以AB为直径的圆交BC于D,则图中阴影部分面积为
[ ]


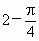
科目:初中数学 来源: 题型:解答题
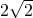 ,⊙A的半径为1,如图所示.若点O在
,⊙A的半径为1,如图所示.若点O在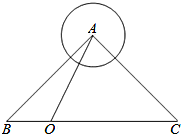 BC上运动(与点B、C不重合),设BO=x,△AOC的面积为y.
BC上运动(与点B、C不重合),设BO=x,△AOC的面积为y.科目:初中数学 来源: 题型:
如图所示,在△ABC中,∠C=90°,
AD是 ∠BAC的平分线,DE⊥AB交AB于E,
F在AC上,BD=DF.
证明:(1)CF=EB.(2)AB=AF+2EB.

科目:初中数学 来源: 题型:
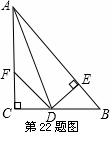
如图所示,在△ABC中,∠C=90°,
AD是 ∠BAC的平分线,DE⊥AB交AB于E,
F在AC上,BD=DF.
证明:(1)CF=EB.(2)AB=AF+2EB.

科目:初中数学 来源: 题型:
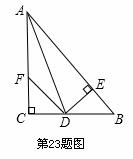
如图所示,在△ABC中,∠C=90°, AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.
证明:(1)CF=EB.(2)AB=AF+2EB.
科目:初中数学 来源: 题型:
如图所示,在△ABC中,∠C=90°, AD是∠BAC的平分线,DE⊥AB交AB于E,
F在AC上,BD=DF.
证明:(1)CF=EB;(2)AB=AF+2EB.
![]()
科目:初中数学 来源: 题型:
如图所示,在△ABC中,∠C=90°,
AD是 ∠BAC的平分线,DE⊥AB交AB于E,
F在AC上,BD=DF.
证明:(1)CF=EB.(2)AB=AF+2EB.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com