
科目:初中数学 来源:北大附中题库 七年级数学(上、下学期用)、测试卷二十 第二学期期末检测(二) 题型:022
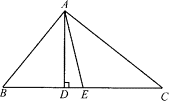
如图所示,已知AD,AE分别是△ABC的高和中线.AB=6,AC=8,BC=10,∠CAB=90°.则:(1)AD=________.(2)![]() =________.(3)△ACE和△ABE的周长差=________.
=________.(3)△ACE和△ABE的周长差=________.
科目:初中数学 来源: 题型:
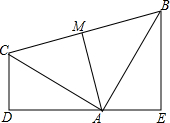 如图所示,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.问:
如图所示,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.问:| 1 | 2 |
科目:初中数学 来源: 题型:
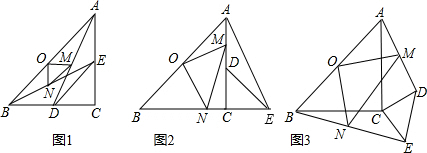
科目:初中数学 来源: 题型:解答题
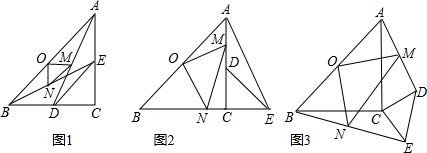
科目:初中数学 来源:2012年辽宁省鞍山市铁东区华育中学中考数学一模试卷(解析版) 题型:解答题

科目:初中数学 来源: 题型:

科目:初中数学 来源: 题型:解答题
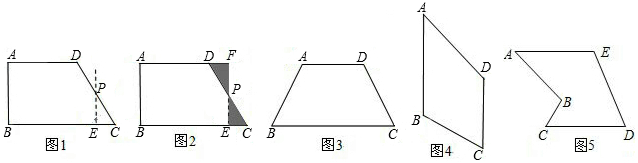
科目:初中数学 来源:不详 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com