| 如下图,在等边△ABC中,D、E、F分别为AB、BC、CA上一点(不是中点),且AD=BE=CF,若每三个三角形两两全等为一组,则图中全等的三角形组数为 |

|
A.3组
B.4组
C.5组
D.6组 |
相关习题
科目:初中数学
来源:安徽省月考题
题型:单选题
如下图,在等边△ABC中,D、E、F分别为AB、BC、CA上一点(不是中点),且AD=BE=CF,若每三个三角形两两全等为一组,则图中全等的三角形组数为
A.3组
B.4组
C.5组
D.6组
查看答案和解析>>
科目:初中数学
来源:期中题
题型:单选题
如下图,在等腰△ABC中,∠ABC=120°,点P是底边AC上一个动点,M、N分别是AB、BC的中点,若PM+PN的最小值为2,则△ABC的周长是
A.2
B.
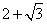
C.4
D.

查看答案和解析>>
科目:初中数学
来源:
题型:
如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN的中点,CD,BD的延长线分别交

于AB,AC于点E,点F,下列结论正确的是( )
①MN的长是BC的
;
②△EMD的面积是△ABC面积的
;
③EM和FN的长度相等;
④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形.
查看答案和解析>>
科目:初中数学
来源:2009-2010学年重庆市东城中学九年级(上)期末数学试卷(解析版)
题型:选择题
如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN的中点,CD,BD的延长线分别交于AB,AC于点E,点F,下列结论正确的是( )
①MN的长是BC的

;
②△EMD的面积是△ABC面积的

;
③EM和FN的长度相等;
④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形.

A.①②⑤
B.①③④
C.①②④
D.①③⑤
查看答案和解析>>
科目:初中数学
来源:第24章《图形的相似》好题集(37):24.4 中位线(解析版)
题型:选择题
如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN的中点,CD,BD的延长线分别交于AB,AC于点E,点F,下列结论正确的是( )
①MN的长是BC的

;
②△EMD的面积是△ABC面积的

;
③EM和FN的长度相等;
④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形.

A.①②⑤
B.①③④
C.①②④
D.①③⑤
查看答案和解析>>
科目:初中数学
来源:2009-2010学年重庆市一中九年级(上)期末数学试卷(解析版)
题型:选择题
如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN的中点,CD,BD的延长线分别交于AB,AC于点E,点F,下列结论正确的是( )
①MN的长是BC的

;
②△EMD的面积是△ABC面积的
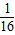
;
③EM和FN的长度相等;
④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形.
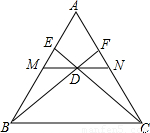
A.①②⑤
B.①③④
C.①②④
D.①③⑤
查看答案和解析>>
科目:初中数学
来源:不详
题型:单选题
如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN的中点,CD,BD的延长线分别交

于AB,AC于点E,点F,下列结论正确的是( )
①MN的长是BC的
;
②△EMD的面积是△ABC面积的
;
③EM和FN的长度相等;
④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形.
查看答案和解析>>
科目:初中数学
来源:
题型:单选题
如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN的中点,CD,BD的延长线分别交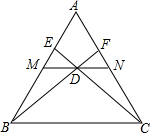 于AB,AC于点E,点F,下列结论正确的是
于AB,AC于点E,点F,下列结论正确的是
①MN的长是BC的 ;
;
②△EMD的面积是△ABC面积的 ;
;
③EM和FN的长度相等;
④图中全等的三角形有4对;
⑤连接EF,则四边形EBCF一定是等腰梯形.
- A.
①②⑤
- B.
①③④
- C.
①②④
- D.
①③⑤
查看答案和解析>>
科目:初中数学
来源:山东省期中题
题型:解答题
如下图,在△ABC中,∠B=90°,点P从A点开始沿AB边向点B以1厘米/秒的速度移动,点Q从B点开始沿BC边向点C以2厘米/秒的速度移动。
(1)如果P、Q分别从A、B两点同时出发,经过几秒钟,△PBQ的面积等于8厘米2?
(2)如果P、Q两分别从A、B两点同时出发,并且P到B又继续在BC边上前进,Q到C后又继续在CA边上前进,设P,Q运动时间为t秒,当6≤t≤9时,△PCQ的面积能否为12.6厘米2?若能,请求出t的値;若不能,请说明理由。
查看答案和解析>>
科目:初中数学
来源:初中数学解题思路与方法
题型:044
如下图,在边长为a的等边△ABC三边BC、CA、AB上分别有点P、Q、R在其中运动,且满足BP+CQ+AR=a,设BP=AR=x,△PQR的面积为S,求S与x之间的函数关系式.

查看答案和解析>>



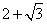

 于AB,AC于点E,点F,下列结论正确的是( )
于AB,AC于点E,点F,下列结论正确的是( ) ;
; ;
;
 ;
; ;
;
 ;
;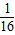 ;
;
 于AB,AC于点E,点F,下列结论正确的是( )
于AB,AC于点E,点F,下列结论正确的是( ) 于AB,AC于点E,点F,下列结论正确的是
于AB,AC于点E,点F,下列结论正确的是 ;
; ;
;
