
| 如图,E是正方形ABCD边AD上一点,AE=2cm,DE=6cm,P是对角线BD上的一动点,则AP+PE的最小值是( )cm。 |
|
A.6 B.8 C.10 D.12 |
科目:初中数学 来源: 题型:
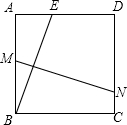 M,交DC于N.
M,交DC于N.科目:初中数学 来源: 题型:
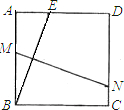 M,交DC于N,设AE=x.
M,交DC于N,设AE=x.科目:初中数学 来源: 题型:

科目:初中数学 来源: 题型:解答题
 M,交DC于N.
M,交DC于N.科目:初中数学 来源: 题型:解答题
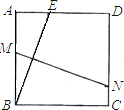 M,交DC于N,设AE=x.
M,交DC于N,设AE=x.科目:初中数学 来源:同步题 题型:解答题
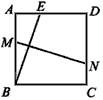
科目:初中数学 来源: 题型:
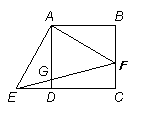
如图,在正方形ABCD中,F是BC上一点,EA⊥AF,AE交CD的延长线于E,连结EF交AD于G.
(1)求证:⊿ABF ≌⊿ADE;(2)求证:BF·FC =DG·EC;(3)若正方形ABCD的边长为![]() ,tg∠BAF=
,tg∠BAF=![]() ,求
,求![]() 的面积.
的面积.
科目:初中数学 来源:第2章《二次函数》常考题集(18):2.6 何时获得最大利润(解析版) 题型:解答题

科目:初中数学 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题

科目:初中数学 来源:第34章《二次函数》中考题集(28):34.4 二次函数的应用(解析版) 题型:解答题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com