
| 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC 与DC重合,得到△DCF,连EF交CD于M,若BC=5,CF=3,则在下列四个结论中: ①CE∥DF; ②△DMF是等腰三角形; ③EF平分∠CFD; ④DM︰MC=4︰3,正确结论的序号是( )。 |
|
A.①②④ B.①③④ C.②③④ D.①②③④ |
科目:初中数学 来源: 题型:
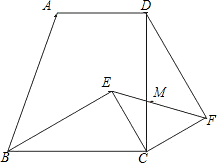 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为( )
如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为( )| A、5:3 | B、3:5 | C、4:3 | D、3:4 |
科目:初中数学 来源: 题型:
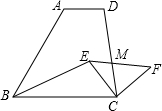 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使B与D重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为
如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使B与D重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,则DM:MC的值为科目:初中数学 来源: 题型:
 16、如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M,若BC=5,CF=3,则在下列四个结论中:①CE∥DF;②△DMF是等腰三角形;③EF平分∠CFD;④DM:MC=4:3.正确结论的序号是
16、如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M,若BC=5,CF=3,则在下列四个结论中:①CE∥DF;②△DMF是等腰三角形;③EF平分∠CFD;④DM:MC=4:3.正确结论的序号是科目:初中数学 来源: 题型:
 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,求DM:MC的值.
如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,求DM:MC的值.科目:初中数学 来源: 题型:解答题
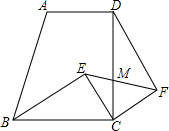 如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,求DM:MC的值.
如图,直角梯形ABCD中,∠BCD=90°,AD∥BC,BC=CD,E为梯形内一点,且∠BEC=90°,将△BEC绕C点旋转90°使BC与DC重合,得到△DCF,连EF交CD于M.已知BC=5,CF=3,求DM:MC的值.科目:初中数学 来源:《第27章 相似》2010年麻城市白果镇第二中学单元测试卷(解析版) 题型:选择题
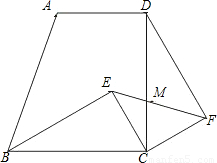
科目:初中数学 来源:第25章《图形的变换》常考题集(09):25.2 旋转变换(解析版) 题型:选择题

科目:初中数学 来源:第25章《图形的变换》中考题集(10):25.2 旋转变换(解析版) 题型:选择题

科目:初中数学 来源:第26章《圆》常考题集(03):26.1 旋转(解析版) 题型:选择题

科目:初中数学 来源:第26章《圆》中考题集(04):26.1 旋转(解析版) 题型:选择题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com