
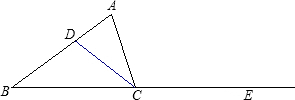
| 如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=( ) |
|
A.150° B.40° C.80° D.90° |
科目:初中数学 来源:不详 题型:单选题
| A.150° | B.40° | C.80° | D.90° |

科目:初中数学 来源: 题型:单选题
 如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=
如图,已知AB=DC,AD=BC,E、F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF=科目:初中数学 来源:黑龙江省月考题 题型:单选题

科目:初中数学 来源: 题型:
 如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC=4
如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC=4| 6 |
A、4
| ||
| B、6 | ||
C、4
| ||
D、2
|
科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:059
已知如图所示,在梯形ABCD中,AB∥DC,AC=DB,AD=BC=4,∠ADC=60°,EF是中位线,交BD于M,交AC于N.

(1)求EF,MN的长及梯形ABCD的面积;
(2)观察MN与梯形上、下底的关系,并思考结论能否推广到一般梯形?
科目:初中数学 来源: 题型:044
如图,已知在等腰三角形ABC中,AB=BC,在AC边上取一点D,延长DC至E,使AD=CE,作EF∥AB,EF=AB,连结DF、DB、FC.
(1)求证:△ABC≌△EFD.
(2)四边形BDFC是平行四边形吗?若是平行四边形,请证明;若不是,请说明理由.

科目:初中数学 来源: 题型:
| ||
| 2 |
科目:初中数学 来源: 题型:解答题
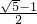 .
.
科目:初中数学 来源:2010-2011学年山东省济南市学林教育培训学校九年级(上)第一次月考数学试卷(解析版) 题型:解答题
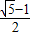 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com