练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知点A（1，2），AC⊥x轴于C，则点C 坐标为

    A.（1，0）
    B.（2，0）
    C.（0，2）
    D.（0，1）

    A
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源： 题型：解答题

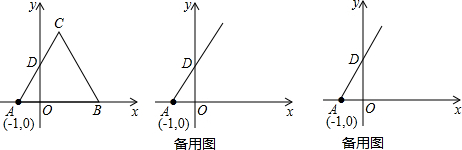
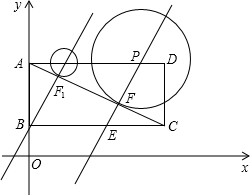    已知：如图，平面直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC=2AB，P为AD边上一动点（P与点A、D不重合），以点P为圆心作⊙P与对角线AC相切于点F，过P、F作直线L，交BC边于点E，当作业宝点P运动到点P1位置时，直线L恰好经过点B，此时直线的解析式是y=2x+1
    （1）BC、AP1的长；
    （2）①求过B、P1、D三点的抛物线的解析式；
    ②求当⊙P与抛物线的对称轴相切时⊙P的半径r的值；
    （3）以点E为圆心作⊙E与x轴相切，当直线L把矩形ABCD分成两部分的面积之比为3：5时，则⊙P和⊙E的位置关系如何？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2012年山东省济南市历下区中考数学一模试卷（解析版） 题型：解答题

    已知：如图，平面直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC=2AB，P为AD边上一动点（P与点A、D不重合），以点P为圆心作⊙P与对角线AC相切于点F，过P、F作直线L，交BC边于点E，当点P运动到点P1位置时，直线L恰好经过点B，此时直线的解析式是y=2x+1
    （1）BC、AP1的长；
    （2）①求过B、P1、D三点的抛物线的解析式；
    ②求当⊙P与抛物线的对称轴相切时⊙P的半径r的值；
    （3）以点E为圆心作⊙E与x轴相切，当直线L把矩形ABCD分成两部分的面积之比为3：5时，则⊙P和⊙E的位置关系如何？并说明理由．

    查看答案和解析>>

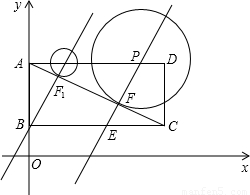
    科目：初中数学 来源：2011-2012学年冀教版九年级（上）期末数学水平测试卷（二）（解析版） 题型：解答题

    已知变量y与x成反比例，它的图象过点A（-2，3）．求：
    （1）反比例函数解析式
    （2）从A（-2，3）向x轴和y轴分别作垂线AB、AC，垂足分别为B、C，则矩形OBAC的面积为______．
    （3）当A点的横坐标为-4时，作AB1、AC1分别垂直于x轴、y轴，B1、C1为垂足，则所得矩形OB1AC1的面积是______．
    （4）将A点在图象上任意移动到点A′，作A′B′、A′C′分别垂直于x轴、y轴，B′、C′为垂足，则所得矩形OB′A′C′的面积是______．
    由此，你可以结合上述信息得出结论是：______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

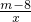    已知反比例函数y=数学公式（m为常数）的图象经过点A（-1，6）．如图，过点A作直线AC与函数y=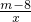数学公式的图象交于点B，与x轴交于点C，且AB=2BC，则点C的坐标为


    1. A.
      （-3，0）
    2. B.
      （-4，0）
    3. C.
      （-5，0）
    4. D.
      （-6，0）

    查看答案和解析>>

    科目：初中数学 来源：河南省期末题 题型：填空题

    已知直线y=﹣x+3与x轴、y轴分别交于A、B两点，点C（0，n）是y轴上一点，把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标是_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知点A（-1，0），点B（与A不重合）在射线AO上，点C在x轴上方，且△ABC为等边三角形，射线AC交y轴于D．
    （1）当AB=4时，则点B、C、D的坐标分别是：B：
    （3，0）
    （3，0）
    ，C：
    （1，2
    		3
    ）
    （1，2
    		3
    ）
    ，D：
    （0，
    		3
    ）
    （0，
    		3
    ）
    ；
    （2）若AB=m（m＞0），则点B、C的坐标分别是：B：
    （m-1，0）
    （m-1，0）
    ，C：
    （
    1
    2
    m-1，
    		3
    2
    m）
    （
    1
    2
    m-1，
    		3
    2
    m）
    ；
    当C、D不重合时，请根据m的不同取值，对于过B、C、D三点的二次函数开口方向作出判断，直接写出结论（不要求证明）．
    （3）是否存在点B，使S△BCD=
    3
    		3
    16
    ？若存在，求出点B的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：单选题

    已知点A（1，2），AC⊥x轴于C，则点C 坐标为
    [     ]

    A.（1，0）
    B.（2，0）
    C.（0，2）
    D.（0，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    27、如图，已知在直角梯形AOBC中，AC∥OB，CB⊥OB，OB=18，BC=12，AC=9，对角线OC、AB交于点D，点E、F、G分别是CD、BD、BC的中点，以O为原点，直线OB为x轴建立平面直角坐标系，则G、E、D、F四个点中与点A在同一反比例函数图象上的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知菱形ABCD的两条对角线AC与BD交于平面直角坐标系的原点，且AD∥x轴，点A的坐标为（-2，3），则点B的坐标为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

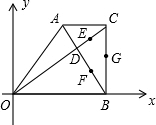    如图，已知在直角梯形AOBC中，AC∥OB，CB⊥OB，OB=18，BC=12，AC=9，对角线OC、AB交于点D，点E、F、G分别是CD、BD、BC的中点，以O为原点，直线OB为x轴建立平面直角坐标系，则G、E、D、F四个点中与点A在同一反比例函数图象上的是点
    （18，6）
    （18，6）
    ．

    查看答案和解析>>


    同步练习册答案